The functional equation of Riemann's zeta function

the functional equation of the Riemann zeta function

and related issues

"This is still perhaps the most important thing we know about the zeta function, as far as its structure..." [Peter Sarnak]

"In his great 1859 paper, "Über die Anzahl der Primzahlen unter eine gegebene Grösse," Riemann gave two proofs of the analytic continuation and functional equation of the zeta function:

Theorem: Let $\Lambda(s)=\pi^{-s/2}\Gamma(s/2)\zeta(s)$ . Then $\Lambda$ has meromorphic continuation to all s, analytic except at simple poles at s = 0 and 1, and satisfies $\Lambda(s)=\Lambda(1-s)$ .

Both proofs are important: the first proof gives the values of the zeta functions at negative odd integers (or, using the functional equation, at positive even integers) while the second proof expresses the zeta function as the Mellin transform of an automorphic form, and leads to the result that $\s(s-s1)\Lambda(s)$ is an entire function of order one. I'll describe the second proof here."

D. Bump, "The Zeta Function" (lecture notes)

"In this paper, Riemann introduces the function of the complex variable t defined by

$\xi(t)=\frac{1}{2}s(s-1)\pi^{-s/2}\Gamma(s/2)\zeta(s)$
with s = 1/2 + it, and shows that $\xi(t)$ is an even entire function of t whose zeros have imaginary part between -i/2 and i/2. He further states, sketching the proof, that in the range between 0 and T the function $\xi(t)$ has about 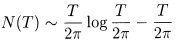$\frac{T}{2\pi}log(\frac{T}{2\pi})-\frac{T}{2\pi}$ zeros...The statement that all of the zeros of the function $\xi(t)$ are real is the Riemann hypothesis."

E. Bombieri, "Problems of the Millenium: The Riemann Hypothesis"

Bernard Julia and others have observed a striking parallel between the functional equation and the Kramers–Wannier duality of statistical mechanics. This was introduced by H. Kramers and G. Wannier in their 1941 paper "Statistics of the Two-Dimensional Ferromagnet" (Physical Review 60, p.252).

In a recent lecture, Marek Wolf stated that the functional equation "is analogous to the Kramers–Wannier duality for the partition function of the two dimensional Ising model with parameter J expressed in units of kT (i.e. equal to interaction constant divided by kT)

$Z(J)=2^{N}(\cosh(J))^{2N}Z(\~{J})$

where N denotes the number of spins and $\~{J}$ is related to J via $e^{-2\~{J}}=\tanh(J)$ . This analogy is a starting point for a series of papers where attempts to find the appropriate spin model possessing the partition function $Z(\beta)$ expressed by the $\zeta(s)$ were undertaken..."

In his article "Statistical theory of numbers", Julia elaborates on the functional equation:

"If one calls the theta function of the one-dimensional lattice one has:

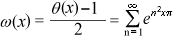
and one can show for Re(s) > 1 the remarkable formula:

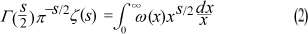
The Poisson summation formula implies (partly) the modularity of the theta function and leads to

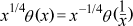
This translates through eq. (2) and the definition

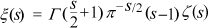
into the functional equation (a physicist would say the "duality") of Riemann:

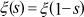
Let us note however that the definition of

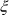cancelled unnaturally and by brute force the pole at s = 1, the multiplication of eq. (2) by s(s - 1)/2 however preserved the symmetry about the axis Re(s) = 1/2."

Later in the same article, Julia writes "It is tantalizing to try to identify the functional equation of Riemann with a duality a la Kramers–Wannier. In the example of the two dimensional (canonical) Ising model we have a (grand-canonical) lattice gas model where the chemical potential is the exterior magnetic field and the nearest neighbour coupling a short range interaction, the spin is essentially the occupation number. In two dimensions and at zero chemical potential the duality relates values of zeta near s = infinity and near s = 0. The critical temperature is left invariant by the duality!"

D. Klusch, "The sampling theorem, Dirichlet series and Hankel transforms", Journal of Computational and Applied Mathematics 44 (1992) 261-273

[abstract:] "Some very surprising relations between fundamental theorems and formulas of signal analysis, of analytic number theory and of applied analysis are presented. It is shown that generalized forms of the classical Whittaker-Kotelnikov-Shannon sampling theorem as well as of the Brown-Butzer-SplettstöBer approximate sampling expansion for non-band-limited signal functions can be deduced via the theory of Dirichlet series with functional equations from a new summation formula for Hankel transforms. This counterpart to Poisson's summation formula is shown to be essentially 'equivalent' to the famous functional equation of Riemann's zeta-function, to the 'modular relation' of the theta-function, to the Nielsen-Doetsch summation formula for Bessel functions and to the partial fraction expansion of the periodic Hilbert kernel."

B.W. Ninham and B.D. Hughes, "Möbius, Mellin, and mathematical physics", Physica A: Statistical and Theoretical Physics 186 (1992) 441-481

[abstract:] "We examine some results and techniques of analytic number theory which have application, or potential application, in mathematical physics. We consider inversion formulae for lattice sums, various transformations of infinite series and products, functional equations and scaling relations, with selected applications in electrostatics and statistical mechanics. In the analysis, the Mellin transform and the Riemann zeta function play a key role."

B. Dragovich, "Adelic harmonic oscillator", Int. J. Mod. Phys. A 10 (1995) 2349-2365

[abstract:] "Using the Weyl quantization we formulate one-dimensional adelic quantum mechanics, which unifies and treats ordinary and p-adic quantum mechanics on an equal footing. As an illustration the corresponding harmonic oscillator is considered. It is a simple, exact and instructive adelic model. Eigenstates are Schwartz-Bruhat functions. The Mellin transform of a simplest vacuum state leads to the well known functional relation for the Riemann zeta function. Some expectation values are calculated. The existence of adelic matter at very high energies is suggested."

B. Dragovich, "On generalized functions in adelic quantum mechanics", Integral Transforms and Special Functions 6 (1998) 197-203.

[abstract:] "Some aspects of adelic generalized functions, as linear continuous functionals on the space of Schwartz-Bruhat functions, are considered. The importance of adelic generalized functions in adelic quantum mechanics is demonstrated. In particular, adelic product formula for Gauss integrals is derived, and the connection between the functional relation for the Riemann zeta function and quantum states of the harmonic oscillator is stated."

P.G. Rooney, "Another proof of the functional equation for the Riemann zeta function", Journal of Mathematical Analysis and Applications 185 (1994) 223-228

[abstract:] "A new proof of the functional equation for the Riemann zeta function is given, based on the theory of Mellin multiplier transformations."

A. Ossicini, "An alternative form of the functional equation for Riemann's zeta function", Atti Semin. Mat. Fis. Univ. Modena e Reggio Emilia 56 (2008–2009) 95–111

[abstract:] "In this paper we present a simple method for deriving an alternative form of the functional equation for Riemann's Zeta function. The connections between some functional equations obtained implicitly by Leonhard Euler in his work "Remarques sur un beau rapport entre les series des puissances tant directes que reciproques" in Memoires de l'Academie des Sciences de Berlin 17, (1768), permit to define a special function, named $A(s)$, which is fully symmetric and is similar to Riemann's "XI" function. To be complete we find several integral representations of the $A(s)$ function and as a direct consequence of the second integral representation we obtain also an analytic continuation of the same function using an identity of Ramanujan."

A. Ossicini, "An alternative form of the functional equation for Riemann's zeta function, II", Acta Univ. Palacki. Olomuc., Fac. rer. nat., Mathematica 53 no. 2 (2014) 115–138

[abstract:] "This paper treats about one of the most remarkable achievements by Riemann, that is the symmetric form of the functional equation for $\zeta(s)$. Riemann provides two different proofs of this. We present here, after showing the first one, a new, simple and direct proof of the symmetric form of the functional equation for both the Eulerian zeta function and the alternating Zeta function, connected with odd numbers. A proof that Euler himself could have arranged with a little step at the end of his paper 'Remarques sur un beau rapport entre les séries des puissances tant direct que réciproches'. This more general functional equation gives origin to a special function, here named ${\cyr \E}(s)(s)$, which we prove that it can be continued analytically to an entire function over the whole complex plane using techniques similar to those of the second proof of Riemann. Moreover we are able to obtain a connection between the Jacobi's imaginary transformation and an infinite series identity of Ramanujan. Finally, after studying the analytical properties of the function ${\cyr \E}(s)(s)$, we complete and extend the proof of a fundamental theorem, both on the zeros of Riemann zeta function and on the zeros of Dirichlet beta function, using also the Euler–Boole summation formula."

A. Saldivar, N.F. Svaiter and C.A.D. Zarro, "Functional equations for regularized zeta-functions and diffusion processes" (preprint 04/2020)

[abstract:] "We discuss modifications in the integral representation of the Riemann zeta-function that lead to generalizations of the Riemann functional equation that preserves the symmetry $s\to (1-s)$ in the critical strip. By modifying one integral representation of the zeta-function with a cut-off that does exhibit the symmetry $x\mapsto 1/x$, we obtain a generalized functional equation involving Bessel functions of second kind. Next, with another cut-off that does exhibit the same symmetry, we obtain a generalization for the functional equation involving only one Bessel function of second kind. Some connection between one regularized zeta-function and the Laplace transform of the heat kernel for the Euclidean and hyperbolic space is discussed."

L. Smith and P. Diaconis, "Honest Bernoulli excursions", Journal of Applied Probability 25 (1988) 464-477

[abstract:] "For simple random walk on the integers, consider the chance that the walk has travelled distance $k$ from its start given that its first return is at time $2n$. We derive a limiting approximation accurate to order $1/n$. We give a combinatorial explanation for a functional equation satisfied by the limit and show this yields the functional equation of Riemann's zeta function"

M.W. Coffey, "Theta and Riemann xi function representations from harmonic oscillator eigensolutions", Phys. Lett. A 362 (2007) 352-356

[abstract:] "From eigensolutions of the harmonic oscillator or Kepler-Coulomb Hamiltonian we extend the functional equation for the Riemann zeta function and develop integral representations for the Riemann xi function that is the completed classical zeta function. A key result provides a basis for generalizing the important Riemann-Siegel integral formula."

J. Baez, This Week's Finds in Mathematical Physics week 217 includes very helpful discussion of the Riemann Hypothesis, Extended Riemann Hypothesis, Grand Riemann Hypothesis, Weil Conjectures, Langlands Programme, the functional equations of zeta and L-functions, modularity of theta functions, etc.

Here are some speculative writings from J.-F. Burnol on another possible physical interpretation of the functional equation.

some related notes on Fourier analysis and the functional equation by B.J. Green

WWN notes on functional equations of L-functions and assorted zeta functions (part of a work-in-progress)

background on the Gamma function

number theory and physics archive prime numbers: FAQ and resources
mystery new search home