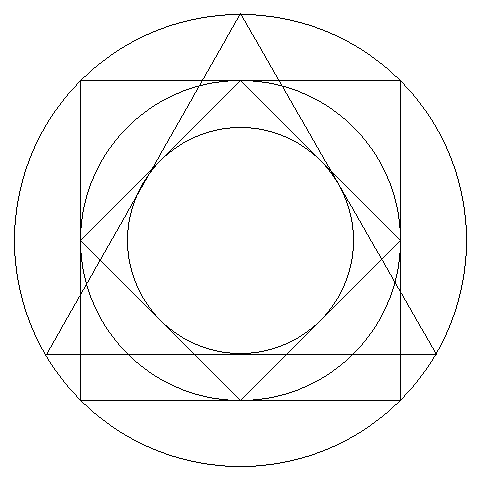
---

The possibility of this diagram depends on two easily proved geometrical facts:

1. A circle circumscribed about an equilateral triangle has an area four times greater than that of a circle inscribed in the same equilateral triangle.
2. A circle circumscribed about a square has an area twice as great as that of a circle inscribed in the same square.

It follows from these facts that a circle inscribed in a square inscribed in a circle inscribed in a square inscribed in a given circle has the same area as a circle inscribed in an equilateral triangle inscribed in the given circle. And since all these figures have the same centre, the two innermost circles coincide.

---

Back to Antony Galton's page of odds and ends.