



Next: Resistant statistics
Up: Descriptive statistics for univariate
Previous: Descriptive statistics for univariate
Contents
Numerical summaries of univariate data, such as the heights in the
previous table, are useful for making quantitative comparisons with
other samples. The following quantities are of paramount interest:
- Sample size is the number of objects making up the sample.
It is also the number of rows
 in the data matrix. It strongly
determines the power of inferences made from the sample
about the original population from which the sample was taken.
For example, sample statistics based on a sample with only 11 people
are not likely to be very representative of statistics for the whole
population of meteorologists at the University of Reading.
in the data matrix. It strongly
determines the power of inferences made from the sample
about the original population from which the sample was taken.
For example, sample statistics based on a sample with only 11 people
are not likely to be very representative of statistics for the whole
population of meteorologists at the University of Reading.
- Central Location is the typical average value about which the
sampled values are located.
In other words, a typical size for the variable based on the sample.
It can be measured in many different ways, but one of the most obvious and
simplest is the arithmetic sample mean:
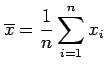 |
|
|
(2.1) |
For the example of height in the previous table, the sample mean is
equal to 174.3cm which gives an idea of the typical height of
meteorologists in Reading.
- Scale is a measure of the spread of the sampled values about
the central location. The simplest measure of the spread is the
range,
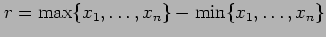 ,
equal to the difference between the largest
value and the smallest value in the sample. This
quantity, however, is based on only the two most extreme objects
in the sample and ignores information from the other
,
equal to the difference between the largest
value and the smallest value in the sample. This
quantity, however, is based on only the two most extreme objects
in the sample and ignores information from the other 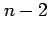 objects
in the sample. A more democratic measure of the spread is given
by the standard deviation
objects
in the sample. A more democratic measure of the spread is given
by the standard deviation
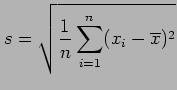 |
|
|
(2.2) |
which is the square root of the sample variance.
2.2
- Shape of the sample distribution can be summarized by
calculating higher moments about the mean such as
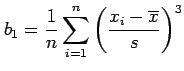 |
|
|
(2.3) |
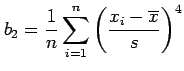 |
|
|
(2.4) |
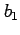 is called the moment measure of skewness and
measures the asymmetry of the distribution.
is called the moment measure of skewness and
measures the asymmetry of the distribution.
 is the moment measure of kurtosis and measures
the flatness of the distribution.
is the moment measure of kurtosis and measures
the flatness of the distribution.




Next: Resistant statistics
Up: Descriptive statistics for univariate
Previous: Descriptive statistics for univariate
Contents
David Stephenson
2005-09-30
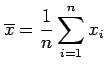
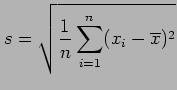
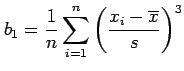
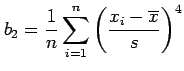
![]() is called the moment measure of skewness and
measures the asymmetry of the distribution.
is called the moment measure of skewness and
measures the asymmetry of the distribution.
![]() is the moment measure of kurtosis and measures
the flatness of the distribution.
is the moment measure of kurtosis and measures
the flatness of the distribution.