



Next: How is probability defined?
Up: Basic probability concepts
Previous: Events and event space
Contents
A random variable,  , is a label allocated to a random event
, is a label allocated to a random event 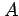 (e.g.
(e.g. 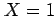 if a tornado occurs and
if a tornado occurs and 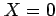 otherwise).
In statistical literature, random variables are often abbreviated
by ``r.v.'' and are denoted by upper case letters (e.g.
otherwise).
In statistical literature, random variables are often abbreviated
by ``r.v.'' and are denoted by upper case letters (e.g.  ).
Actual observations (samples) of a particular random variable
are denoted by the corresponding lower case letter (e.g.
).
Actual observations (samples) of a particular random variable
are denoted by the corresponding lower case letter (e.g. 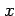 ).
In other words,
).
In other words, 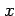 is a possible value that random variable
is a possible value that random variable  can take. Data
can take. Data  , ...,
, ..., 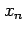 making up a sample can often be
thought of as repeated observations of the same random variable
making up a sample can often be
thought of as repeated observations of the same random variable  .
.
Random variables can either be categorical, discrete numbers
(i.e. integers), or continuous numbers (i.e. real numbers).
Categorical variables can either be nominal (no ordering)
e.g. {sun}, {rain}, {snow}, or cardinal (ordered)
e.g.
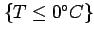 ,
,
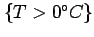 .
Discrete random variables can be binary (e.g.
.
Discrete random variables can be binary (e.g. 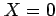 or
or 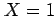 )
or can be count variables (e.g.
)
or can be count variables (e.g.
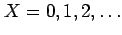 ) representing
the number of events (e.g. number of hurricanes).
The probability
) representing
the number of events (e.g. number of hurricanes).
The probability
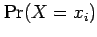 of a random variable
of a random variable  taking different observable values,
taking different observable values, 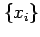 defines
the probability distribution discussed in the
next chapter.
defines
the probability distribution discussed in the
next chapter.




Next: How is probability defined?
Up: Basic probability concepts
Previous: Events and event space
Contents
David Stephenson
2005-09-30
![]() ,
,
![]() .
Discrete random variables can be binary (e.g.
.
Discrete random variables can be binary (e.g. ![]() or
or ![]() )
or can be count variables (e.g.
)
or can be count variables (e.g.
![]() ) representing
the number of events (e.g. number of hurricanes).
The probability
) representing
the number of events (e.g. number of hurricanes).
The probability
![]() of a random variable
of a random variable ![]() taking different observable values,
taking different observable values, ![]() defines
the probability distribution discussed in the
next chapter.
defines
the probability distribution discussed in the
next chapter.