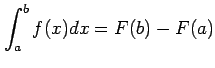Next: Empirical estimates
Up: Distributions of continuous variables
Previous: Distributions of continuous variables
Contents
Because there is an infinite continuum of possible values 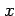 for
a continuous random variable
for
a continuous random variable  , the probability of
, the probability of  being
exactly equal to a particular value is zero
being
exactly equal to a particular value is zero
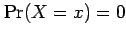 !
Therefore, the approach used to define the probability distribution
of discrete random variables can not be used to describe the distribution
of continuous random variables.
Instead, the probability distribution of a continuous
variable is defined by the probability of a random variable
being less than or equal to a particular value
!
Therefore, the approach used to define the probability distribution
of discrete random variables can not be used to describe the distribution
of continuous random variables.
Instead, the probability distribution of a continuous
variable is defined by the probability of a random variable
being less than or equal to a particular value
The probability distribution function, 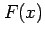 , is
close to zero for large negative values of
, is
close to zero for large negative values of 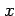 and
increases towards one for large positive values of
and
increases towards one for large positive values of 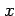 .
.
The probability distribution function is sometimes referred to
more specifically as the cumulative distribution function (c.d.f).
The probability of a continuous random variable  being
in a small interval
being
in a small interval
![$ (a,a+\delta x]$](img208.png) is given by
is given by
The derivative of the probability distribution,
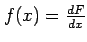 ,
is known as the probability density function (p.d.f.) and can
be integrated with respect to
,
is known as the probability density function (p.d.f.) and can
be integrated with respect to 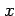 to find the probability of
to find the probability of  being
in any interval
being
in any interval
In other words, the probability of  being in a certain interval
is simply given by the integrated area under the probability
density function curve.
being in a certain interval
is simply given by the integrated area under the probability
density function curve.




Next: Empirical estimates
Up: Distributions of continuous variables
Previous: Distributions of continuous variables
Contents
David Stephenson
2005-09-30
![]() being
in a small interval
being
in a small interval
![]() is given by
is given by
![$\displaystyle F(a+\delta x)-F(a)\approx \left[\frac{dF}{dx}
\right]_{x=a}\delta x$](img210.png)