



Next: Sampling distributions
Up: Parameter estimation
Previous: Parameter estimation
Contents
Imagine that we assume a certain random variable to be distributed
according to some distribution
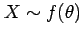 and that we wish
to use a sample of data to estimate the population parameter
and that we wish
to use a sample of data to estimate the population parameter 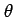 .
For example, we may be interested in estimating either the mean
.
For example, we may be interested in estimating either the mean 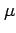 or the variance
or the variance  (or both) of a variable that is thought to be
normally distributed
(or both) of a variable that is thought to be
normally distributed
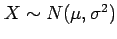 .
A single value point estimate
.
A single value point estimate
 may be obtained
by choosing a suitable sample statistic
may be obtained
by choosing a suitable sample statistic
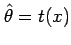 , for example, the
sample mean
, for example, the
sample mean
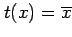 provides a simple (yet far from unique) way
of estimating the population mean
provides a simple (yet far from unique) way
of estimating the population mean 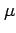 .
However, because sample sizes are finite, the sample estimate is only
an approximation to the true population value - another sample from
the same population would give a different value for the same sample
statistic.
Therefore, rather than give single value point estimates, it is better
to use the information in the sample to provide a range of possible
values for
.
However, because sample sizes are finite, the sample estimate is only
an approximation to the true population value - another sample from
the same population would give a different value for the same sample
statistic.
Therefore, rather than give single value point estimates, it is better
to use the information in the sample to provide a range of possible
values for 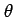 known as an interval estimate.
To take account of the sampling uncertainty caused by finite
sample size, it is necessary to consider the probability distribution
of sample statistics in more detail.
known as an interval estimate.
To take account of the sampling uncertainty caused by finite
sample size, it is necessary to consider the probability distribution
of sample statistics in more detail.




Next: Sampling distributions
Up: Parameter estimation
Previous: Parameter estimation
Contents
David Stephenson
2005-09-30