



Next: A legal example
Up: Motivation
Previous: Motivation
Contents
The previous chapter on estimation showed how it is possible
to use sample statistics to make estimates of population
parameters that include estimates of sampling uncertainty.
However, sometimes we would like to go further and use
sample statistics to test the binary true/false validity of
certain hypotheses (assumptions) about population parameters.
In other words, we want to make true/false decisions about
specified hypotheses based on the evidence provided by the
sample of data. This ``Sherlock Holmes'' detective approach
is obviously more risky than simply estimating parameters, but is
often used to clarify conclusions from scientific work.
In fact, the radical idea underlying the
whole of natural science is that hypotheses and theories
are not only judged by their intrinsic beauty but can also
be tested for whether or not they explain observed data.
This is exemplified by the Royal Society's
6.1 revolutionary
famous motto ``nullis in verba'', which is taken
from a poem by the roman poet Horace and means do
not (unquestioningly) accept the words (or theories) of anyone !
Suppose, for example, we suspect there might be a non-zero
correlation between two variables (e.g. sunspot numbers
and annual rainfall totals in Reading).
In other words, our scientific hypothesis 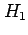 is that the
true (population) correlation between these two variables is non-zero.
To test this hypothesis, we examine some data and find a
sample correlation with, let's imagine, a quite large value.
Now did this non-zero sample correlation arise because
the hypothesis
is that the
true (population) correlation between these two variables is non-zero.
To test this hypothesis, we examine some data and find a
sample correlation with, let's imagine, a quite large value.
Now did this non-zero sample correlation arise because
the hypothesis 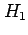 is really true, or did it just happen by
chance sampling ?
The hypothesis that the large sample value happened just by
chance is known as the null hypothesis
is really true, or did it just happen by
chance sampling ?
The hypothesis that the large sample value happened just by
chance is known as the null hypothesis 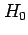 .
In order to claim that the alternative hypothesis
.
In order to claim that the alternative hypothesis 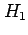 is true, we must first show that the large value would
be very unlikely to happen by pure chance.
In other words, we must use the data to reject the null
hypothesis
is true, we must first show that the large value would
be very unlikely to happen by pure chance.
In other words, we must use the data to reject the null
hypothesis 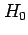 in favour of the more scientifically interesting
alternative hypothesis
in favour of the more scientifically interesting
alternative hypothesis 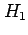 .
By using the data to reject
.
By using the data to reject 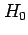 , we are able to make a binary
decision about which of the two hypotheses is least inconsistent
with the data.
, we are able to make a binary
decision about which of the two hypotheses is least inconsistent
with the data.




Next: A legal example
Up: Motivation
Previous: Motivation
Contents
David Stephenson
2005-09-30
![]() is that the
true (population) correlation between these two variables is non-zero.
To test this hypothesis, we examine some data and find a
sample correlation with, let's imagine, a quite large value.
Now did this non-zero sample correlation arise because
the hypothesis
is that the
true (population) correlation between these two variables is non-zero.
To test this hypothesis, we examine some data and find a
sample correlation with, let's imagine, a quite large value.
Now did this non-zero sample correlation arise because
the hypothesis ![]() is really true, or did it just happen by
chance sampling ?
The hypothesis that the large sample value happened just by
chance is known as the null hypothesis
is really true, or did it just happen by
chance sampling ?
The hypothesis that the large sample value happened just by
chance is known as the null hypothesis ![]() .
In order to claim that the alternative hypothesis
.
In order to claim that the alternative hypothesis ![]() is true, we must first show that the large value would
be very unlikely to happen by pure chance.
In other words, we must use the data to reject the null
hypothesis
is true, we must first show that the large value would
be very unlikely to happen by pure chance.
In other words, we must use the data to reject the null
hypothesis ![]() in favour of the more scientifically interesting
alternative hypothesis
in favour of the more scientifically interesting
alternative hypothesis ![]() .
By using the data to reject
.
By using the data to reject ![]() , we are able to make a binary
decision about which of the two hypotheses is least inconsistent
with the data.
, we are able to make a binary
decision about which of the two hypotheses is least inconsistent
with the data.