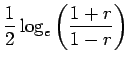Z-test for unpaired equal correlations

Next: Further reading Up: Two sample tests Previous: F-test for equal variances Contents

Do two samples come from populations with the same correlation ?

$\displaystyle H_0:\rho_1$	$\displaystyle =$	$\displaystyle \rho_2$	(6.9)
$\displaystyle H_1: \rho_1$	$\displaystyle \neq$	$\displaystyle \rho_2 \nonumber$

The trick here is to transform correlations into variables that are approximately normally distributed by using Fisher's Z transformation

$\displaystyle Z$

$\displaystyle =$

$\displaystyle \frac{1}{2}\log_e\left(\frac{1+r}{1-r}\right)$

(6.10)

The variance of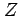

is independent of

and is given by

. The hypotheses can now be tested easily by using a 2-sample Z-test on unpaired means of normally distributed variables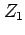

and

$\displaystyle Z$

$\displaystyle =$

$\displaystyle \frac{\overline{Z_1}-\overline{Z_2}}{s_p}\sim N(0,1)$

where the pooled estimate of variance is given by

$\displaystyle s_p^2$

$\displaystyle =$

$\displaystyle s_1^2+s_2^2=\frac{1}{n_1-3}+\frac{1}{n_2-3}$

Next: Further reading Up: Two sample tests Previous: F-test for equal variances Contents

David Stephenson 2005-09-30