
prime numbers, the zeta function and li
Firstly, this page has nothing to do with the logarithmic integral function Li(x) which is defined by

Similarly, it has nothing to do with the mathematician Xian-Jin Li who has reformulated the Riemann hypothesis.
It is about an ancient Chinese concept called li and its possible
relevance to our understanding of the distribution of primes.
I first came across the concept in 1991, in this excerpt from p.15 of Alan Watts' beautiful book Tao: The Watercourse Way (Pantheon, 1975):
"I have practiced Chinese calligraphy for many years, and am not
yet a master of the art, which could be described as dancing with
brush and ink on absorbent paper. Because ink is mostly water,
Chinese calligraphy - controlling the flow of water with the soft
brush as distinct from the hard pen - requires that you go with the
flow. If you hesitate, hold the brush too long in one place, or
hurry, or try to correct what you have written, the blemishes are
all too obvious. But if you write well there is at the same time the
sensation that the work is happening on it own, that the brush is
writing all by itself - as a river, by following the line of least
resistance, makes elegant curves. The beauty of Chinese calligraphy
is thus the same beauty which we recognize in moving water, in foam,
spray, eddies, and waves, as well as in clouds, flames and weavings
of smoke in sunlight. The Chinese call this kind of beauty the
following of li, an ideogram which referred originally to the
grain in jade and wood, and which Needham translates as "organic
pattern," although it is more generally understood as the "reason" or
"principle" of things. Li is the pattern of behaviour which
comes about when one is in accord with the Tao, the watercourse of
nature. The patterns of moving air are of the same character, and so
the Chinese idea of elegance is expressed as feng-liu, the
flowing of wind."
This is from another essay
by A. Watts on Taoism:
"The tao is a certain kind of order, and this kind of order is not
quite what we call order when we arrange everything geometrically in
boxes, or in rows. That is a very crude kind of order, but when you
look at a plant it is perfectly obvious that the plant has order. We
recognize at once that it is not a mess, but it is not symmetrical and it
is not geometrical looking. The plant looks like a Chinese drawing,
because they appreciated this kind of non-symmetrical order so much
that it became an integral aspect of their painting. In the Chinese
language this is called li, and the character for li
means the markings in jade. It also means the grain in wood and the
fiber in muscle. We could say, too, that clouds have li, marble
has li, the human body has li. We all recognize it, and
the artist copies it whether he is a landscape painter, a portrait
painter, an abstract painter, or a non-objective painter. They all are
trying to express the essence of li. The interesting thing is,
that although we all know what it is, there is no way of defining it.
Because tao is the course, we can also call li the watercourse,
and the patterns of li are also the patterns of flowing water.
We see those patterns of flow memorialized, as it were, as sculpture
in the grain in wood, which is the flow of sap, in marble, in bones,
in muscles. All these things are patterned according to the basic
principles of flow. In the patterns of flowing water you will find all kind
of motifs from Chinese art, immediately recognizable, including the
S-curve in the circle of yang-yin.
So li means then the order of flow, the wonderful dancing
pattern of liquid, because Lao-tzu likens tao to water:
The great tao flows everywhere, to the left and to the right, It
loves and nourishes all things, but does not lord it over them." At the end of the 1990's, I was spontaneously struck by an
extraordinary mental image – that of a 'dynamical history' underlying the
familiar distribution of prime numbers. The mental image seemed to imply a sort of
evolutionary process in which the prime numbers were seen to be moving particles in
a 1-dimensional continuum, eventually coming to rest when they
collectively achieved the dynanical equilibrium of their familiar
configuration.
In the following years, while attempting to write about certain (more
widely acknowledged) mysteries associated with the prime numbers and
Riemann zeta function,
and in particular about the sort of aesthetic
reactions people tend to have to them, I invoked the notion of li.
As I then understood it, it was typified by the kind of beauty associated with mists, clouds, smoke, rugged mountain
ranges, gnarled trees, etc.
In 2003, Wooden
Books (who published my little
reference book) brought out a book called Li: Dynamic Form in Nature by architect David Wade. In the introduction he explains:
"Li are essentially dynamic formations, and as such can
give the impression of a frozen moment, of a process caught at a
particular instant of time..."
Wade's section on 'brechiated' li observes that
"The aesthetic appeal...owes much to...the impression
they convey of frozen activity, which seems to present a snapshot of
intense formative processes from the remote geological past."
The 'contornare' section, featuring physiographical configurations
refers to
"...well-delineated boundaries [wherein] the topography
is more strongly revealed, clearly exposing the imprint of the active
formation processes involved ."
The highlighted quotes above struck me as hugely relevant to my
fleeting impressions concerning the primes, so I decided to put together
this webpage dedicated to the 'Li-ness' of the distribution of primes, and
of the (intimately related) Riemann zeta function.
The seeming 'Li-ness' of the primes and zeta, is to me,
another major piece of the 'prime number evolution' puzzle. This subtle,
unquantifiable aspect of their appearance suggests that they have
been (and I use the past tense very loosely here!) 'in motion'. That was
the initial flash of insight. I didn't make the connection with li at the
time - that came a couple of years later. And when I did, it was
Alan Watts' description I had in mind. The characteristic
of li which David Wade describes above hadn't occurred to me.
Here are some other quotes from Li: Dynamic Form in Nature
which may be relevant to the distribution of prime numbers:
From the introduction:
"Li are appealing in a purely aesthetic sense
because, although they tend to be relatively simple configurations,
they have a high degree of content."
In the section dedicated to 'anfractuous' li, he writes:
"In common with many li, the processes by which
these forms come into being can sometimes be traced back to structures
associated with their underlying causation, and sometimes not; the reasons
for this are still mysterious.
It is also the case that they may appear at every level of scale,
from the micro- to the macroscopic, a fact that provides additional
testimony to their essentially archetypal nature." The section on 'angulated' li states:
"The aesthetic appeal that links each of these
examples...derives from the attractive combination of geometry and
pure chance."
In his book Number Theory in Science and Communication, M.
Schroeder argues that the distribution of primes, with its blend
of structure and apparent randomness possess the necessary ingredients
for aesthetic appeal.
Wade quotes the Taoist sage Chhen Shun (c. 1200C.E.
), who wrote that li
"derive from a natural and inescapable law of affairs and
things that arise directly out of the nature of the universe."
Compare this to the following statement made by Bertrand Russell,
which applies particularly directly to the properties of the integers:
"Mathematics takes us still further from what is human, into
the region of absolute necessity, to which not only the actual world,
but every possible world must conform."
A section of the stalk of a dead nettle is displayed, revealing
"...a curiously irregular cell structure that appears
to vacillate between the various possible systems of orderly close
packing. In fact, the appearance of such disturbances is the distinguishing
mark of li; perfectly ordered arrays belong to the domain of
pure symmetry."
This description brings to mind the delicate balance between order and disorder
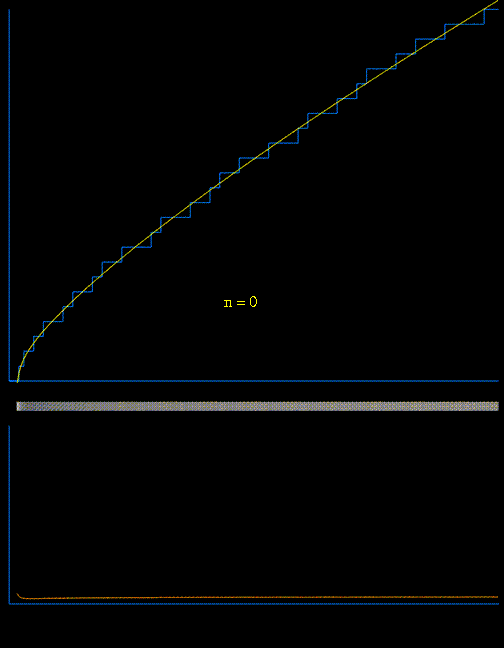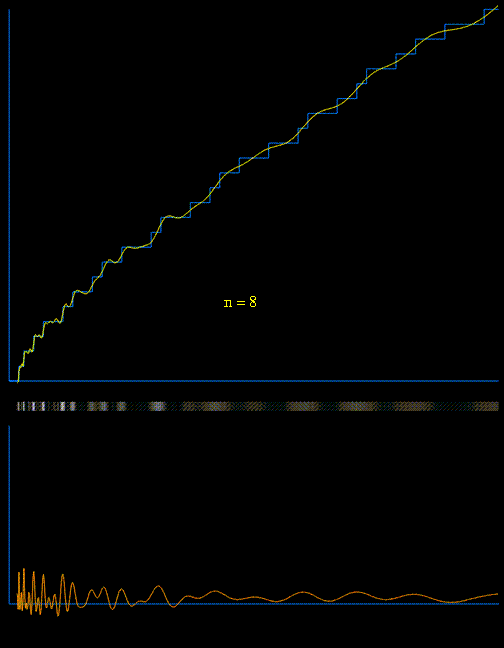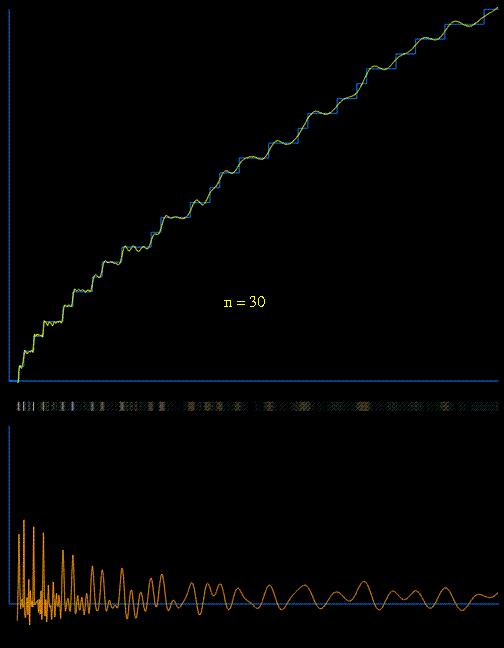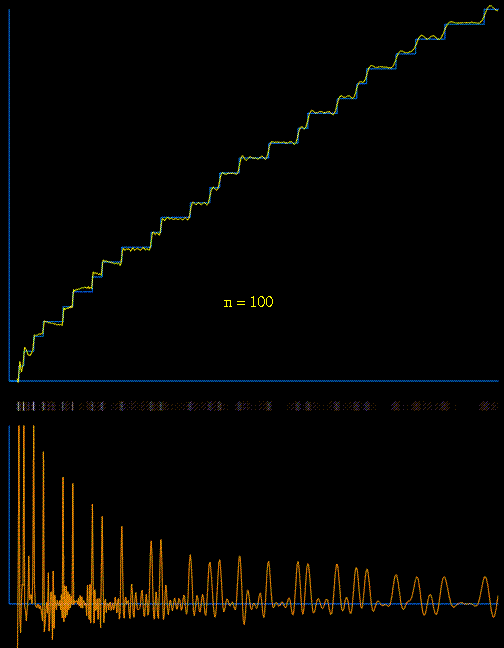
evident in the distribution of primes. In the graph below, a vertical step occurs
above each prime number along the horizontal axis. Note that the Greek letter
π is being used in a different context than the familiar 3.14... which
relates circumferences and diameters of circles. Here π(x) indicates
the number of primes less than or equal to a given number x.
Wade's section on "ripples and dunes" mentions forms which
"...appear to have an existence of their own, governed
by laws of their own....
The abiding characteristics of these formations, common to many
li, is the sense of an overall order, showing clear repetitive
features, but lacking a strict periodicity." The last sentence immediately brings to mind the Prime Number
Theorem which tells us that the primes have an overall order
(a tendency to 'thin out' at a predictable logarithmic rate),
although they are well known to be lacking a strict periodicity.
* * * The following images all reveal some aspect of the structure of
the distribution of primes or the (intimately related) Riemann zeta
function:
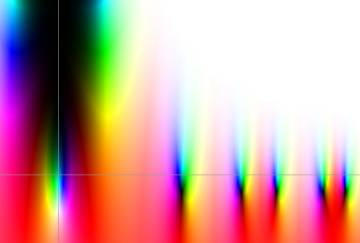
This image was reproduced from Prof. Marcus du Sautoy's
Music of the
Primes website, which ties in with his acclaimed book of the
same title. The image is not explained, but it has almost certainly
been produced from the structure of the Riemann zeta function. Note
that the colour scheme has been added later as an aesthetic touch and appears
not to be mathematically relevant.
This graphic
by J.-F. Colonna was generated from the sequence of primes. Although the algorithm used
is somewhat contrived, the overall 'li-ness' evident here is a reflection of the
'li-ness' of the sequence of primes. Note that the seeming horizontal and
vertical symmetries are not strictly upheld, but merely suggested
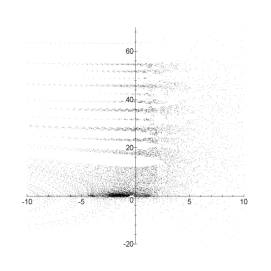
This is an old graphic from
E.
Weisstein's Mathworld generated from the modulus of the
Riemann zeta function. The spikes correspond to the nontrivial zeros,
the irregularity of their spacing being particularly evident at this scale.
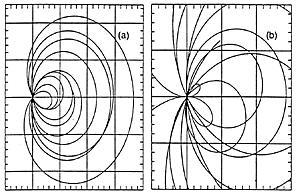
2-dimensional representations of the Riemann zeta
function using colours, by Alex Astashyn who produced them using a Mathematica
application developed by Bernd Thaller (University of Graz).
graphic
by J.-F. Colonna generated from the Riemann zeta function
from "The Newtonian orbits of the Riemann zeta function"
by N. Guffey and N. Petulante
Here we see the result of the
Riemann zeta function acting on various pieces of the critical
line Re[s] = 1/2, the graphs coming from
"Phase of the Riemann
zeta function and the inverted harmonic oscillator" by R. Bhaduri,
A. Khare and J. Law.
a graph of the function
R(x) – π(x) showing the deviation of the prime distribution from its average behaviour
Here's another (seemingly fractal) prime-generated image
from A. Leatherland.
Another representation of part of the Riemann zeta
function. You should bear in mind that, as the complex plane extends infinitely in all
directions, any graph of the zeta function which can be physically produced can never
show more than an infinitesimal part of the zeta function's overall behaviour. Any 'li-ness'
present is therefore only ever hinted at. According to Voronin's
Universality Theorem the zeta function, if we look far enough, will replicate virtually
any behaviour of any part of any analytic function, to arbitrary accuracy, infinitely
often! Woon has
deduced from this that the zeta function is in some sense a fractal object.
Another window on the Riemann zeta function (origin unknown).
This animation shows the way in which the exact distribution
of primes, as represented by the function π(x), can be constructed from
a simple function plus a succession of sinusoidal functions (waveforms) whose frequencies
are directly related to the roots of the Riemann zeta function. It is fully
explained here.
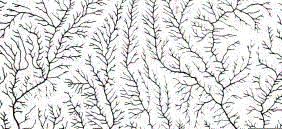
* * * A section on river drainage systems in David Wade's book Li contains
a fascinating insight, which seems fitting here:
"With the formation of the river systems there is a
certain paradox of priority; rivers shape the landscape, and the
landscape contains the river. But, like the chicken and egg riddle, it
is unclear which came first. There is, in fact, a distinct sense of
the inevitability of such forms, a view that if carried through credits
them with the almost Platonic noumenon of preexistence."























Jungian archetypes and prime numbers
number theory and physics archive prime numbers FAQ and resources inexplicable secrets of creation
home page

