[Review article from SIAM Review, 41, No.2 (1999) 236-266]

Abstract

Comparison between formulae for the counting functions of the heights t_n of the Riemann zeros and of semiclassical quantum eigenvalues E_n suggests that the t_n are eigenvalues of an (unknown) hermitean operator H, obtained by quantizing a classical dynamical system with hamiltonian H_cl. Many features of H_cl are provided by the analogy; for example, the "Riemann dynamics" should be chaotic and have periodic orbits whose periods are multiples of logarithms of prime numbers. Statistics of the t_n have a similar structure to those of the semiclassical E_n; in particular, they display random-matrix universality at short range, and nonuniversal behaviour over longer ranges. Very refined features of the statistics of the t_n can be computed accurately from formulae with quantum analogues. The Riemann-Siegel formula for the zeta function is described in detail. Its interpretation as a relation between long and short periodic orbits gives further insights into the quantum spectral fluctuations. We speculate that the Riemann dynamics is related to the trajectories generated by the classical hamiltonian H_cl = XP.

1. Introduction

Our purpose is to report on the development of an analogy, in which three areas of mathematics and physics, usually regarded as separate, are intimately connected. The analogy is tentative and tantalizing, but nevertheless fruitful.. The three areas are eigenvalue asymptotics in wave (and particularly quantum) physics, dynamical chaos, and prime number theory. At the heart of the analogy is a speculation concerning the zeros of the Riemann zeta function (an infinite sequence of numbers encoding the primes): the Riemann zeros are related to the eigenvalues (vibration frequencies, or quantum energies) of some wave system, underlying which is a dynamical system whose rays or trajectories are chaotic.

Identification of this dynamical system would lead directly to a proof of the celebrated Riemann hypothesis. We do not know what the system is, but we do know many of its properties, and this knowledge has brought insights in both directions: from mathematics to physics, by stimulating the development of new spectral asymptotics, and from physics to mathematics, by indicating previously unsuspected correlations between the Riemann zeros. We have review some of this material before [1,2,3,4,5,6], but these accounts do not include several recent developments to be described here, especially those in the last part of section 4 and all of sections 5 and 6.

To motivate the approach from physics, we begin with the counting function for the primes, pi(x), defined as the number of primes less than x (thus pi(3.5)=2); this is a staircase function, with unit steps at the primes p. The density of primes is the distribution

At the roughest level of description, and with the distribution appropriately smoothed,

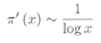
(as implied by the prime number theorem: pi(x) ~ x/logx).

One of Riemann's great achievements [7,8] was to give exact formula for pi'(x), constructed as follows. First pi'(x) is expressed in terms of a function J(x) [7, Chap.1] that has jumps at prime powers:

(see section 1.18 of [7]). Here the numbers t_n in the oscillatory contributions are related to the complex Riemann zeros, defined as follows.

Riemann's zeta function, depending on the complex variable s, is defined as

and by analytic continuation elsewhere in the s plane. It is known that the complex zeros (i.e, those with nonzero imaginary part) of zeta(s) lie in the "critical strip" [Re s between 0 and 1], and the Riemann hypothesis states that in fact all these zeros lie on the "critical line" Res = 1/2 (see Figure 1). The numbers t_n in (1.4) are defined by

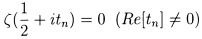0

If the Riemann hypothesis is true, all the (infinitely many) t_n are real, and are the heights of the zeros above the real s axis. It is known by computation that the first 1,500,000,001 complex zeros lie on the line [9], as do more than one-third of all of them [10].

Each term in the sum (1.4) describes an oscillatory contribution to the fluctuations of the density of primes, with larger Ret_n corresponding to higher frequencies.

FIGURE 1

Because of the logarithmic dependence, each oscillation gets slower as x increases. This slowing-down can be eliminated by the change of variable u = log x; thus

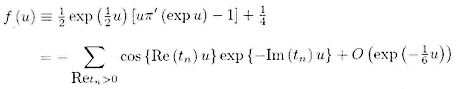
If the Riemann hypothesis is true, Im t_n = 0 for all n, and the function f(u), constructed from the primes, has a discrete spectrum; that is, the support of its Fourier transform is discrete. If the Riemann hypothesis is false, this is not the case. The frequencies t_n are reminiscent of the decomposition of a musical sound into its constituent harmonics. Therefore there is a sense in which we can give a one-line nontechnical statement of the Riemann hypothesis: "The primes have music in them."

However, readers are cautioned against thinking that it would be easy to hear this prime music by constructing f(u) as defined in (1.7) and then converting it into an audio signal. In order for the human ear to hear the lowest Riemann zero, with t₁ = 14.13…, it would be necessary to play N ~ 100 periods of cos(t₁u), requiring primes in the range [ x between 0 and exp(2pi N/t₁) ~ exp(45) ~ 10¹⁹].

On this acoustic analogy, the heights t_n (hereinafter referred to simply as "the zeros") are frequencies. This raises the compelling question: frequencies of what? A natural answer would be: frequencies of some vibrating system. Mathematically, such frequencies - real numbers - are discrete eigenvalues of a self-adjoint (hermitean) operator. That the search for such an operator might be a fruitful route to proving the Riemann hypothesis is an old idea, going back at least to Hilbert and Polya [7]; what is new is the physical interpretation of this operator and the detailed information now available about it.

The mathematics of almost all eigenvalue problems encountered in wave physics is essentially the same, but the richest source of such problems is quantum mechanics, where the eigenvalues are the energies of stationary states ("levels"), rather than frequencies as in acoustics or optics, and the operator is the hamiltonian. Reflecting this catholicity of context, we will refer to the t_n interchangeably as energies or frequencies, and the operator as H (Hilbert, Hermite, Hamilton…).

To help readers navigate through this review, here is a brief description of the sections. In section 2 we describe the basis of the Riemann-quantum analogy, which is an identification of the periodic orbits in the conjectured dynamics underlying the Riemann zeros, made by comparing formulae for the counting functions of the t_n and of asymptotic quantum eigenvalues. Section 3 explains the significance of the long periodic orbits in giving rise to universal (that is, system-independent) behaviour in classical and semiclassical mechanics and, by analogy, the Riemann zeros. The application of these ideas to the statistics of the zeros and quantum eigenvalues is taken up in section 4. Section 5 is a description of a powerful method for calculating the t_n (the Riemann-Siegel formula), with a physical interpretation in terms of resurgence of long periodic orbits that implies new interpretations of the periodic-orbit sum for quantum spectra. The properties of the conjectured dynamical system are listed in section 6, where it is speculated that the zeros are eigenvalues of some quantization of the dynamics generated by the hamiltonian H_cl = XP.

2. The Analogy

3. Long Orbits and Universality

4. Periodic-Orbit Theory for Spectral Statistics

5. Riemann-Siegel Formulae

6. Spectral Speculations

References

[1] M.V.Berry, Riemann's zeta function: A model for quantum chaos, in Quantum Chaos and Statistical Nuclear Physics, T.H. Seligman and H. Nishioka, eds., Lecture Notes in Phys. 263, Springer-Verlag, New York, 1986, pp. 1-17.

[2] M.V.Berry, Quantum chaology (the Bakerian lecture), Proc. Roy. Soc. Lond. Ser. A, 413 (1987) pp. 183-198.

[3] M.V. Berry, Some quantum-to-classical asymptotics, in Chaos and Quantum Physics, Les Houches Lecture Series 52, M.-J. Giannoni, A. Voros, and J. Zinn-Justin, eds., North-Holland, Amsterdam, 1991, pp.251-304.

[4] J.P.Keating, The Riemann zeta-function and quantum chaology, in Quantum Chaos, G. Casati, I. Guarneri, and V. Smilansky, eds. North-Holland, Amsterdam, 1993, pp. 145-185.

[5] J.P.Keating, Periodic orbits, spectral statistics, and the Riemann zeros, in Supersymmetry and Trace Formulae: Chaos and Disorder, J.P. Keating, D.E.Khmelnitskii, and I.V.Lerner, eds., Plenum, New York, 1998, pp. 1-15.

[6] M.V.Berry and J.P.Keating, H = xp and the Riemann zeros, in Supersymmetry and Trace Formulae: Chaos and Disorder, J.P. Keating, D.E.Khmelnitskii, and I.V.Lerner, eds., Plenum, New York, 1998, pp.355-367

[7] H.M.Edwards, Riemann's Zeta Function, Academic Press, New York, London, 1974

[8] D. Zagier, The first 50 million prime numbers, Math. Intelligencer, 0 (1977), pp. 7-19.

[9] J. Van de Lune, H.J.J. te Riele, and D.T.Winter, On the zeros of the Riemann zeta function in the critical strip. IV, Math. Comp., 46 (1986), pp. 667-681.

[10] N. Levinson, More than one third of the zeros of Riemann's zeta-function are on rho = 1/2, Adv. Math., 13 (1974), pp. 383-436.