an approximate logarithmic spiral generated by the distribution of primes
The prime number theorem, which describes the approximate rate at which the prime numbers 'thin out' tells us that

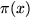 is the number of primes less than or equal to x.
is the number of primes less than or equal to x.
The fact that the primes are in this way 'logarithmically distributed' can be exploited in order to construct an approximate logarithmic spiral from the primes themselves.
Recall that a logarithmic (or equiangular) spiral can be described most easily in polar coordinates as:
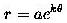
 which looks like this:
which looks like this:
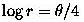

We can also rearrange the PNT formula as follows:
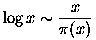

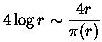
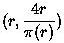
To clarify - at radial distance r from the origin, we plot a point whose angular measure (in radians) is given by 4r divided by the number of primes less than r.
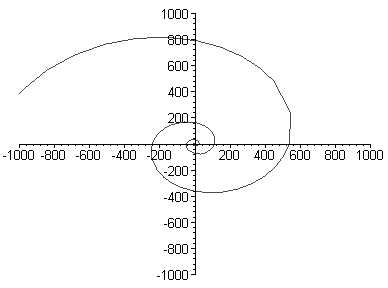
Below we see this plot over four different ranges, and how it quite clearly produces an approximate spiral which appears to 'smooth itself out' as the range increases.



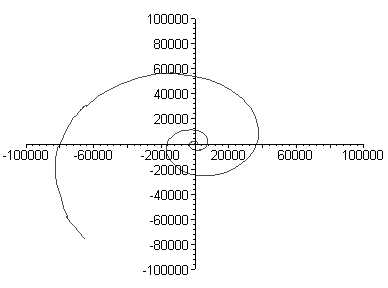
It is important to note that these 'spirals' are generated without
any direct reference to a logarithm. The only 'input' is the data contained in
the prime counting function 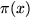 , i.e the locations
of the actual prime numbers themselves. The 'jaggedness' is indicative
of the extent to which the prime counting function deviates from the
smooth, approximating function x/logx.
, i.e the locations
of the actual prime numbers themselves. The 'jaggedness' is indicative
of the extent to which the prime counting function deviates from the
smooth, approximating function x/logx.
We should also note that the choice a = 1 and k = 1/4 was arbitary. Different choices would also produce approximations of logarithmic spirals. Changing a has the effect of rotating the spiral, while k controls the rate at which the spiral 'opens out'.
Often, when explaining the basic facts of the distribution of primes to interested non-mathematicians, I come up against a significant obstacle:
The primes thin out, asymptotically, at a particular rate (this much people can generally understand), but the rate is governed by a logarithm, and the public at large has no real understanding of what a logarithm is. The most familiar manifestation of the logarithm is the logarithmic spiral, visible in snailshells, seashells, etc. For this reason, I often resort to saying something like "The rate at which the primes thin out is related to the rate at which a snailshell uncoils.".
Although mathematically unremarkable, nothing like the above images have
ever been published anywhere that I am aware of. I feel that they provide
a very pleasing illustration of my favoured explanation, and may perhaps
provide those people unable (or unwilling) to grasp the concept of a logarithm
an opportunity to witness directly the beauty of the prime number
theorem.
It might help to imagine actually physically marking these figures out on a plane. Suppose we were to mark out x and y axes, and concentric circles centred at the origin of radii 1, 2, 3, 4,... up to some sufficiently large integer.
We then imagine ourselves walking out along the positive x axis, counting the primes we find. As we arrive at each circle of radius n, we divide n2 by the number of primes we have found up to that point, and walk that many 'steps' in an anticlockwise direction around the circle. The steps must be of constant length, but that can be any size we like (to make the 'spirals' seen here, our steps would have to be 4 units each - different sized steps will produce spirals which open out at different rates). Arriving at this point on the circle of radius n, we mark a point on the plane.
We then return to the point n on the positive x axis, and continue walking out along the x axis, counting primes, and marking a point on each circle in this way. This will generate figures like those seen above.
This might actually make quite a nice piece of 'land art', involving
the placing of stones or the planting of trees, if anyone feels motivated
to actually carry this out.
tutorial archive mystery home contact