
the "encoding" of the distribution of prime numbers by the nontrivial
zeros of the Riemann zeta function [elegant approach]
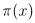 simply gives the
number of primes less than or equal to x. The prime
number theorem states that
simply gives the
number of primes less than or equal to x. The prime
number theorem states that  .
This is already evident in a graph of
.
This is already evident in a graph of
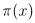 for x
ranging from 0 to 1000:
for x
ranging from 0 to 1000:

This asymptotic relation given by the Prime Number Theorem suggests that there might exist some alternative, logarithmically-weighted prime counting function which is simply asymptotic to x. This turns out to be the case.
Chebyshev introduced
the function  , which counts not
just primes, but also all powers of primes. Each pk for
k = 1, 2, 3, ... is counted with weight log p. Formally we
write
, which counts not
just primes, but also all powers of primes. Each pk for
k = 1, 2, 3, ... is counted with weight log p. Formally we
write

Where
 are the
von Mangoldt
values.
These vanish for n which are not the power of some prime, and take
the value log p when n is a power of prime p:
are the
von Mangoldt
values.
These vanish for n which are not the power of some prime, and take
the value log p when n is a power of prime p:

It isn't difficult to show the equivalence of the statements
 . The
proof of the Prime Number Theorem usually involves proving the latter.
. The
proof of the Prime Number Theorem usually involves proving the latter.
In many ways,  is the more natural counting function.
It seems that we should think of primes (and their powers) as having an
intrinsic logarithmic weight. In his classic text The Distribution of
Prime Numbers, Ingham states:
is the more natural counting function.
It seems that we should think of primes (and their powers) as having an
intrinsic logarithmic weight. In his classic text The Distribution of
Prime Numbers, Ingham states:
"It happens that of the three functions,
,
, the one which arises most naturaly from the analytical point of view is the one most remote from the original problem, namely
. For this reason it is usually most convenient to work in the first instance with
...to deduce results about
. This is a complication which seems inherent in the subject, and the reader should familiarise himself at the outset with the function
, which is to be regarded as the fundamental one."
[Note: 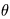 is
another function introduced by Chebyshev related to the distribution of
primes.]
is
another function introduced by Chebyshev related to the distribution of
primes.]
"[medaevil philosopher] William of Occam, elevated to a method the idea that when one must choose between two explanations, one should always choose the simpler. Occam's razor, as the principle is called, cuts out the difficult and chooses the simple. When things get too complicated, it sometimes makes sense to stop and wonder: Have I asked the right question? Here the choice is between two functions that count primes: one is the function psi(x), approximated by a straight line, and the second is pi(x), approximated by the curving function Li(x). Surely William of Occam would have chosen to study psi(x)."
E. Bombieri from "Prime Territory: Exploring the Infinite Landscape at the Base of the Number System" (The Sciences, Sept./Oct. 1992)
Here we see part of the graph of  ,
superimposed over the (asymptotic) function x. If we were to zoom
out far enough, the graph of the former would become indistinguishable from
the latter.
,
superimposed over the (asymptotic) function x. If we were to zoom
out far enough, the graph of the former would become indistinguishable from
the latter.
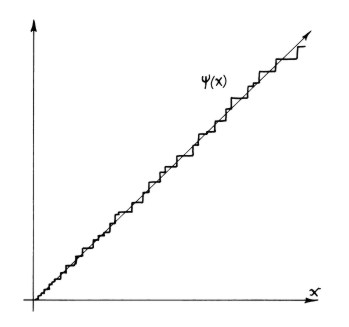
It turns out that the (discontinuous) step function
 can be expressed precisely as the
limit of a sequence of smooth functions which are based on the complex zeros of
the Riemann zeta function.
can be expressed precisely as the
limit of a sequence of smooth functions which are based on the complex zeros of
the Riemann zeta function.
Directly involved in the usual proof of the Prime Number Theorem
is the explicit formula:

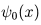 differs very slightly from
differs very slightly from
 in that at points of discontinuity it takes a value halfway between its
limits on either side, a phenomenon
familiar from Fourier analysis.
in that at points of discontinuity it takes a value halfway between its
limits on either side, a phenomenon
familiar from Fourier analysis.
Note that the fourth term in the right-hand side is neglibible for large x and the second is just a constant.
Therefore, we see that the fluctuations of
 about its asymptotic approximation
x are determined by the values
about its asymptotic approximation
x are determined by the values  , which are the
nontrivial zeros of the zeta function, i.e. those with nonzero
imaginary parts. These are all known to lie in the critical strip,
as illustrated below. It is also known that they must be symmetric about
both the real axis and the critical line Re(s) = 1/2.
, which are the
nontrivial zeros of the zeta function, i.e. those with nonzero
imaginary parts. These are all known to lie in the critical strip,
as illustrated below. It is also known that they must be symmetric about
both the real axis and the critical line Re(s) = 1/2.
At present, all known nontrivial zeros lie on the critical line. The Riemann Hypothesis states that they all
must (and it is known that there is an infinite number of them).
Here are some
tables of zeros compiled by Andrew Odlyzko.

Because the  are complex, the values
are complex, the values
 must also be complex. However, this is not a
problem, as the nontrivial zeros are known to come in complex-conjugate pairs
must also be complex. However, this is not a
problem, as the nontrivial zeros are known to come in complex-conjugate pairs
 and
and  . The values
. The values
 and
and
 are also
complex-conjugates, so all imaginary parts cancel in the infinite sum.
are also
complex-conjugates, so all imaginary parts cancel in the infinite sum.
Incidentally the function  maps the positive reals onto a logarithmic spiral in the complex plane.
maps the positive reals onto a logarithmic spiral in the complex plane.
 and
and
 produce "complex-conjugate" spirals (mutual
reflections across the real axis), so each contribution
produce "complex-conjugate" spirals (mutual
reflections across the real axis), so each contribution
 =
2Re[
=
2Re[ ]
]is a real-valued function, a sort of logarithmically-rescaled sinusoid with increasing amplitude as pictured below:
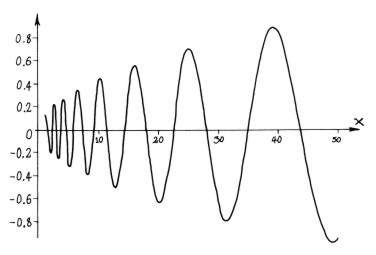
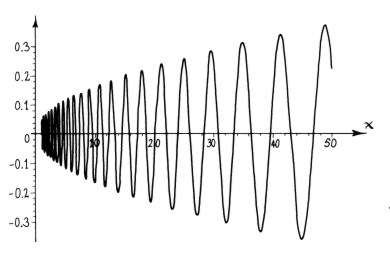
Above we see the contributions from the first and sixth
nontrivial zeros,  = 1/2 + (14.13...)i
and
= 1/2 + (14.13...)i
and  = 1/2 + (37.58...)i.
= 1/2 + (37.58...)i.
These waveforms are related to the logarithmic spirals in the same way that a normal sine waves are related to the unit circle.
If we were to logarithmically rescale the x-axis, these function would
have a constant frequency equal to the imaginary part of  .
The rate of amplitude growth is related to the real part, which in all known
cases is just 1/2.
.
The rate of amplitude growth is related to the real part, which in all known
cases is just 1/2.
Returning to the explicit formula

we see that Chebyshev's logarithmic prime counting function can be reconstructed by starting with the function
 , and then
successively adding "spiral wave" functions
, and then
successively adding "spiral wave" functions

generated by complex-conjugate pairs
 ,
,
 of complex zeta zeros. Below we see an animation
where the first 250 pairs of zeros are used to gradually approximate
of complex zeta zeros. Below we see an animation
where the first 250 pairs of zeros are used to gradually approximate
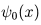 .
.
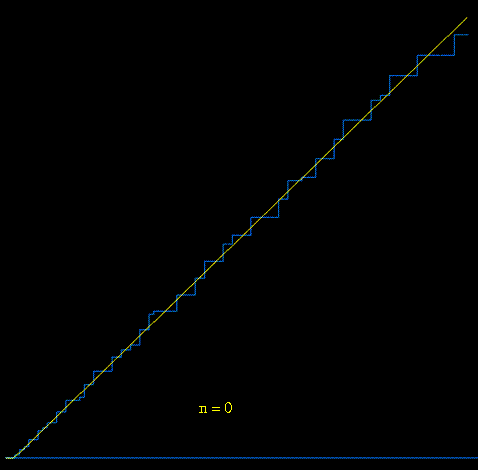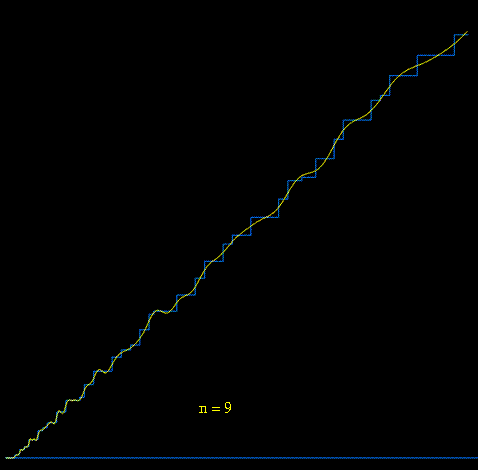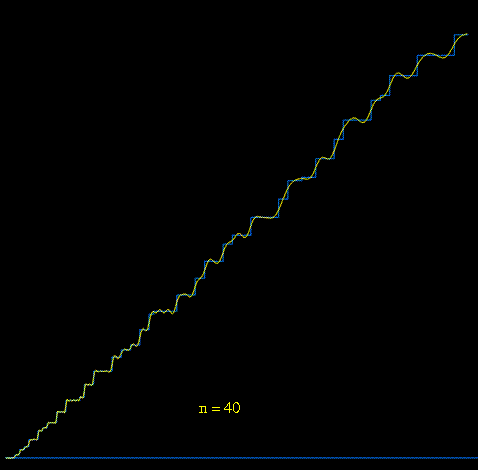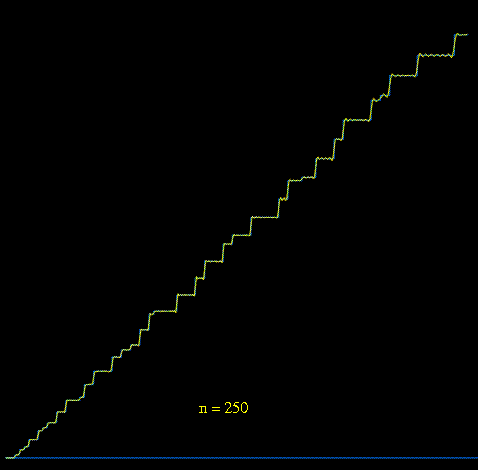
[animation courtesy of Raymond Manzoni]
Glen Pugh, while at the University of British Columbia, developed a more
sophisticated and interactive applet along similar lines. It can be viewed here.
the more common approach
number theory and physics archive prime numbers: FAQ and resources
mystery new search home