"The Lindelöf Hypothesis is an absolutely fascinating hypothesis. It seems that it ought to be provable. It's infinitely easier than the Riemann Hypothesis. Nevertheless, it's way, way beyond anything we can do."

S. Patterson, quoted in Dr. Riemann's Zeros (Atlantic, 2002), p.191

Like the Riemann Hypothesis, the Lindelöf Hypothesis concerns the behaviour of the Riemann zeta function, but the LH is weaker than the RH. That is, the truth of the Riemann Hypothesis implies the truth of the Lindelöf Hypothesis, but not vice versa.

More specificically, the Lindelöf Hypothesis deals with the rate of growth of the Riemann zeta function on the critical line.

A thorough introduction to the subject can be found in Chapter 13 (p.276-281) of [T], from which the following excerpts are taken.
 

We begin with a simple statement of the hypothesis:

Recall that the 'big-O' notation of Landau is such that "f = O(g)" means that |f| < Cg for some positive constant C, over the common domain of definition of f and g.

Here we see a graph of the modulus of zeta on the critical line for t-values up to 500. It is the rate of growth we see here that the LH concerns:

The LH essentially conjectures that this function grows more slowly than any positive power of t.

There are numerous equivalent statements and reformulations of the LH to be found in the literature. We shall look at two of the most important ones.
 

[T] explains that the LH is equivalent to certain statements concerning positive even integer moments of the zeta function. Moments of a function are mean values of the various powers of the function (or its modulus) over large intervals.

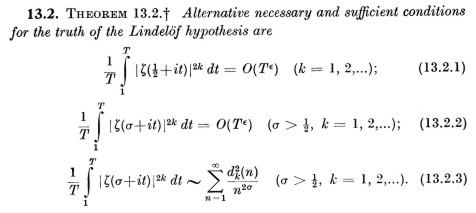
Here the d_k(n) are the Dirichlet coefficients of the k^th power of the zeta function. This result is due to Hardy and Littlewood ([HL1]). Several years earlier they had shown that the 2^nd moment of zeta on the critical line (k = 1, and T tending to infinity) is equal to 1 ([HL2]), which is obviously in agreement with 13.2. In 1926 Ingham ([I]) similarly showed that the 4^th moment = 1/12 (the case k = 2), also in agreement with the result. No further progress was made in this area until some conjectures for higher moments appeared in the 1990's ([CGh], [CGo]).

Most recently, in their paper [KS], J. Keating and N. Snaith presented a conjecture concerning (not necessarily integer or real) moments of the zeta function. They arrived at this through the application of random matrix theory. Their conjecture is consistent with all of the aforementioned results and conjectures, and if it is eventually shown to be correct, the Lindelöf Hypothesis would follow.
 

[T] also includes the following reformulation of the LH. Note that the sum in the RHS is a partial sum of the Dirichlet series of the k^th power of zeta.

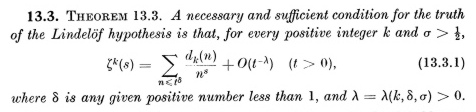
Backlund reformulated the LH in terms of the locations of the zeros of zeta:

[E] summarises this as follows: "The Lindelöf hypothesis is equivalent to the statement that for every \sigma > 1/2, the number of roots in the rectangle {T <= Im s <= T+1, \sigma <= Re s <= 1} grows less rapidly than log T as T -> infinity.", and then points out that "It follows from this that the Riemann hypothesis implies the Lindelöf hypothesis because if the Riemann hypothesis is true, then there are never any zeros in the rectangle in question."

 

In a book review of [KV], P. Sarnak states the Lindelöf Hypothesis as

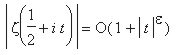
In 1998, N.V. Kuznetsov produced a preprint, claiming to have proved the Lindelöf Hypothesis. This eventually was found to contain errors.

[T] E. Titchmarsh, The Theory of the Riemann Zeta-Function, second edition (Clarendon, Oxford, 1986).

[HL1] G.H. Hardy and J.E. Littlewood, "On Lindelöf's hypothesis concerning the Riemann zeta-function", Proceedings of the Royal Society (A) 103 (1923) 403-412.

[HL2] G.H. Hardy and J.E. Littlewood, "Contributions to the theory of the Riemann zeta-function and the theory of the distribution of primes", Acta Mathematica 41 (1918) 119-196.

[I] A.E. Ingham, "Mean-value theorems in the theory of the Riemann zeta-function", Proceedings of the London Mathematical Society 27 (1926) 273-300.

[CGh] J.B. Conrey and A. Ghosh, "On mean values of the zeta function, iii", from Proceedings of the Amalfi Conference on Analytic Number Theory, Universita di Salerno, 1992.

[CGo] J.B. Conrey and S.M. Gonek, "High moments of the Riemann zeta-function" (1998 preprint)

[KS] J.P. Keating and N.S. Snaith, "Random matrix theory and $\zeta(1/2+it)$", Communications in Mathematical Physics 214 (2000) 57-89.

[B] R. Backlund, "Uber die beziehung zwischen anwachsen und nullstellen der zerafunktion", Ofversigt Finska Vetensk. Soc. 61 (1918-19) No. 9.

[E] H.M. Edwards, Riemann's Zeta Function (Academic Press, 1974).

[KV] A.A. Karatsuba, S.M. Voronin, N. Koblitz, The Riemann Zeta-function (de Gruyter, 1992)