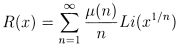Zagier goes on to state:
"There is one more approximation which I would like to mention. Riemann's research on prime numbers suggests that the probability for a large number x to be prime should be even closer to 1/log x if one counted not only the prime numbers but also the powers of primes, counting the square of a prime as half a prime, the cube of a prime as a third, etc. This leads to the approximation

or, equivalently,

The function on the right side...is denoted by R(x), in honour of Riemann. It represents an amazingly good approximation to π(x) as the above values show."To be clear about this, it should be pointed out that the explicit definition for the the function R(x) is