Distribution of primes tutorial

Euler proved that the infinite sum 1 + 1/2 + 1/3 + 1/4 + 1/5 + ^{. . .} does not take a finite value (unlike, say, 1 + 1/2 + 1/4 + 1/8 + ^{. . .} which sums to 2). However, if we raise the denominators to higher powers, for example

1 + 1/2² + 1/3² + 1/4²+ ^{. . .} or 1 + 1/2³ + 1/3³ + 1/4³ + ^{. . .}

we get a computable, finite sum. As it is possible to extend the concept of exponentiation xⁿ from integer n to rational powers, and eventually to all real-valued exponents, we can consider how small x>1 can be made so that

1 + 1/2^x + 1/3^x+ 1/4^x + 1/5^x + ^{. . .}

still converges to a finite sum. It turns out that this sum converges for all x > 1, which then suggests the (real valued) zeta function

ζ(x) = 1 + 1/2^x + 1/3^x + 1/4^x + 1/5^x + ^{. . .}

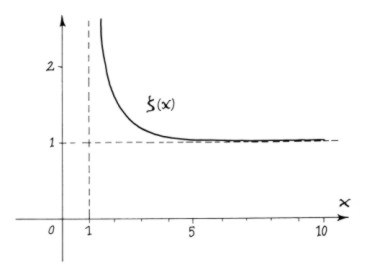
We know that (a) this is a well-defined smooth function for x>1, (b) that its value approaches infinity as x approaches 1 from above, and (c) that as x tends to infinity, ζ(x) approaches 1 (all higher terms dwindle to nothing). Euler demonstrated that this infinite sum could also be expressed in terms of an infinite product using the sequence of prime numbers:

ζ(x) = [1/(1-1/2^x)] [1/(1-1/3^x)][1/(1-1/5^x)][1/(1-1/7^x)]. . .

Formally, we write

$zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^{s}}=\prod_{primes\;\{p\}}\frac{1}{1-p^{-s}}$

Although this identity may be initially surprising, it's not actually that difficult to demonstrate. See for example Keith Devlin's elementary historical account "How Euler discovered the zeta function".

The zeta function, as simple as it is to define, has some remarkable properties, some of which we shall now examine.

<< previous beginning next >>