Here we see the behaviour of the Riemann zeta function on the critical line Re[z] = 1/2. Recall that all known zeros lie on this line. These graphs show parts of the image of this line after it has been mapped into 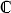by ζ. The nontrivial zeros correspond to the points on the curve where it passes through the origin.

These graphs are taken from the article "Phase of the Riemann zeta function and the inverted harmonic oscillator" by R.K. Bhaduri, Avinash Khare and J. Law in which they state

"The loop structure of the ζ function at σ = 1/2, with some near-circular shapes, is reminiscent of the Argand plots for the scattering amplitudes of different partial waves in the analysis of resonances, for example in pion-nucleon scattering."

This seems to be more than a superficial resemblance, as the authors go on to argue that "The smooth phase of the ζ function along the line of the zeros is related to the quantum density of states of an inverted oscillator." This is just one of a number of surprising connections between physics and prime numbers (in this case via the zeta function).