

R(x –2) + R(x –4) + R(x –6) + . . .
The sum over the nontrivial zeros can be expressed as the sum of the
sequence of functions {–Tk(x)} where
Tk is defined as follows:

Our first apparent obstacle is that ρk and ρ–k are complex numbers. However, the function xk can be meaningfully extended from real k to complex k in a fairly straightforward way. This means that the x ρk and x –ρk are also complex-valued.
This also initially seems like a problem, as the Riemann function R defined earlier as an approximation of π(x) was clearly intended to act on real values only. However, by the same process of analytic continuation discussed earlier, R can be extended to the entire complex plane, taking the form given by the Gram series:

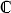 .
Also note the role of the Riemann zeta function.
.
Also note the role of the Riemann zeta function.So we see that R(x ρk) and R(x ρ–k) can be given precise meanings, and will yield complex numbers. Usefully, the imaginary parts of this pair of complex numbers can be shown to cancel, so that their sum which is Tk(x) will always be a real-valued function.
A detailed explanation of how the nontrivial zeros can be used to exactly
reconstruct the function π(x) can be found
here.