The distribution of nontrivial zeros of the zeta function is governed by the following asymptotic law:

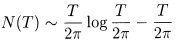
This gives the approximate number of zeros in the critical strip whose imaginary parts are between 0 and T. Using this, we can 'renormalise' the locations of the zeros, so that the average spacing between them becomes 1, and then study the statistics of the local fluctuations.

It has been hypothesised that these statistics correspond to the eigenvalue spacing statistics of a particular class of large random matrices called the Gaussian Unitary Ensemble. GUE statistics are important because they relate to the energy spectra of particular systems studied by quantum chaologists.

This hypothesis is backed up by overwhelming numerical evidence, involving thousands of hours of supercomputer calculations carried out by A. Odlyzko, among others. This makes plausible the spectral interpretation of the Riemann zeta function, which suggests that the imaginary parts ("heights") of the nontrivial zeros correspond to the spectrum of eigenvalues of some operator. The spectral interpretation is among the most promising approaches to proving the Riemann Hypothesis.

Peter Sarnak of Princeton University says, "Odlyzko's computations are the first phenomenological insight that the zeros are absolutely, undoubtedly, "spectral" in nature. Riemann himself would be impressed... At the phenomenological level, this is perhaps the most striking discovery about zeta since Riemann."

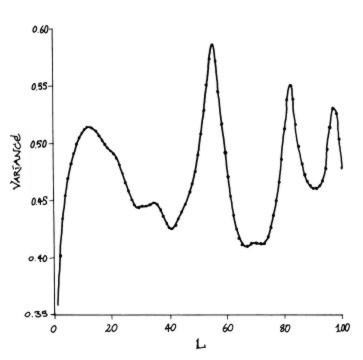
Remarkably, on the basis of his conjecture, and results from quantum chaology, Michael Berry has been able to predict certain subtle statistical trends in the spacing of the nontrivial zeros. These concern their number variance, and have also been confirmed by Odlyzko's calculations. Above we see a graphs displaying how accurately Berry's prediction (the curve) fits the actual data based on the spacings of the zeros (the small black squares).

More information on this quantum chaological approach to proving the Riemann Hypothesis can be found here.