theta functions
Probably the best place to start is R. Bellman's beautiful little book A Brief
Introduction to Theta Functions (Holt, Rinehart and Winston, New York, 1961)
In his article "Statistical theory of numbers",
Julia elaborates on the functional equation of the
Riemann zeta function:
"If one calls
 the theta function of the one-dimensional lattice one has:
the theta function of the one-dimensional lattice one has:
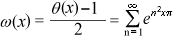
and one can show for Re(s) > 1 the remarkable formula:
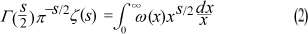
The Poisson summation formula implies (partly) the modularity of the theta function and leads to
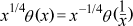
This translates through eq. (2) and the definition
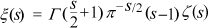
into the functional equation (a physicist would say the "duality") of Riemann:
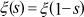
Let us note however that the definition of
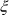 cancelled
unnaturally and by brute force the pole at s = 1, the multiplication
of eq. (2) by s(s - 1)/2 however preserved the symmetry about
the axis Re(s) = 1/2."
cancelled
unnaturally and by brute force the pole at s = 1, the multiplication
of eq. (2) by s(s - 1)/2 however preserved the symmetry about
the axis Re(s) = 1/2."
D. Klusch, "The sampling theorem, Dirichlet series and Hankel transforms", Journal of Computational and Applied Mathematics 44 (1992) 261-273
[abstract:] "Some very surprising relations
between fundamental theorems and formulas of signal analysis, of analytic number theory and of
applied analysis are presented. It is shown that generalized forms of the classical
Whittaker-Kotelnikov-Shannon sampling theorem as well as of the Brown-Butzer-SplettstöBer
approximate sampling expansion for non-band-limited signal functions can be deduced via the
theory of Dirichlet series with functional equations from a new summation formula for Hankel
transforms. This counterpart to Poisson's summation formula is shown to be essentially
'equivalent' to the famous functional equation of Riemann's zeta-function, to the 'modular
relation' of the theta-function, to the Nielsen-Doetsch summation formula for Bessel functions
and to the partial fraction expansion of the periodic Hilbert kernel."
B.W. Ninham and S. Lidin, "Some remarks on quasi-crystal structure", Acta Crystallographica A 48 (1992) 640-650
[abstract:] "The Fourier transform of skeleton delta function that characterizes the most striking features of experimental quasi-crystal diffraction patterns is evaluated. The result plays a role analogous to the Poisson summation formula for periodic delta functions that underlie classical crystallography. The real-space distribution can be interpreted in terms of a backbone comprising a system of intersecting equiangular spirals into which are inscribed (self-similar) gnomons of isoceles triangles with length-to-base ratio the golden mean...In addition to the vertices of these triangles, there is an infinite number of other points that may tile space in two or three dimensions. Other mathematical formulae of relevance are briefly discussed."
[from concluding remarks:] "Perhaps the most interesting feature is that our Fourier-transform
sum seems to have much in common with the distribution of the zeros of the Riemann zeta function...!
That indicates something of the depth of the problem. That the zeta function ought to come into the
scheme of things somehow is not surprising - the Poisson and related summation formulae are
special cases of the Jacobi theta function. [Indeed the Bravais lattices can be enumerated
systematically through an integral over all possible products and sums of products of any
three of the four theta functions in different combinations that automatically preserve
translational and rotational symmetries.] The theta-function transformations are themselves
just another way of writing the [functional equation of the zeta
function]. Additionally, the properties of the zeta function are automatically connected
to the theory of prime numbers. So one expects that the Rogers-Ramanujan relations must
play a central role in the scheme of things for quasi-crystals."
B.W. Ninham and B.D. Hughes, "Möbius, Mellin, and mathematical physics", Physica A: Statistical and Theoretical Physics 186 (1992) 441-481
[abstract:] "We examine some results and techniques of analytic number theory which have application, or potential application, in mathematical physics. We consider inversion formulae for lattice sums, various transformations of infinite series and products, functional equations and scaling relations, with selected applications in electrostatics and statistical mechanics. In the analysis, the Mellin transform and the Riemann zeta function play a key role."
archive tutorial mystery new search home contact