
| Procrustes problems |
|
|
|
|
| RME Home |
| DCS Home |
| Research |
| Teaching |
| Publications |
| Contact |
|
|
| Email me |
The villain Procrustes forced his victims to sleep on an iron bed; if they did not fit the bed he cut off or stretched their limbs to make them fit.
The classical Procrustes matrix problem asks how closely a matrix, A, can be approximated by a second, given, matrix B multiplied by a matrix U with orthonormal columns. This problem has a solution in terms of the polar factor of the AB'. The requirement that U have orthonormal columns can be relaxed to requiring that they are only orthogonal. Problems of this nature arise in the optical imaging of orientation columns and in some Independent Components Analysis algorithms. In this case there is no closed form solution, but it is straightforward to find numerical solutions.
Basis orthogonalization
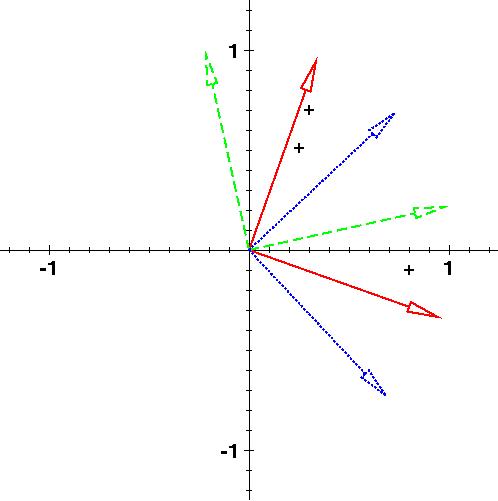
The classical Procrustes problem can be used to find an orthogonal basis for the vectors forming the columns of A. Such an orthogonalization of a basis is associated with the names of Lowdin and Poincare. Unlike the Gram-Schmidt procedure, this basis is democratic in that a permutation of the columns of A yields the same basis vectors - though they may be relabelled.
An alternative basis is provided by the V that minimizes the orthogonal Procrustes problem. This basis is also invariant under permutations of the columns of A, but the relaxation of orthonormality allows the basis to be more closely aligned with the original vectors.'
The picture illustrates this for 3 two-dimensional vectors (marked with crosses) and the bases found by Lowdin orthogonalization (green), the orthogonal Procrustes problem (red), and the first two left singular vectors of A, (blue) which are also known as the principal components, which are aligned with the directions of greatest variance, though in this two-dimensional example the second principal component is completely determined by the requirement that it be orthogonal to the first.
Details of numerical methods for solving the orthogonal Procrustes problem and applications can be found in Orthogonal, but not orthonormal, Procrustes problems.