"...it may be appropriate to quote a statement of Poincaré, who said (partly in jest no doubt) that there must be something mysterious about the normal law since mathematicians think it is a law of nature whereas physicists are convinced that it is a mathematical theorem."

"Consider the integers divisible by both p and q [p and q both prime]. To be divisible by p and q is equivalent to being divisible by pq and consequently the density of the new set is 1/pq. Now, 1/pq = (1/p)(1/q), and we can interpret this by saying that the "events" of being divisible by p and q are independent. This holds, of course, for any number of primes, and we can say using a picturesque but not very precise language, that the primes play a game of chance! This simple, nearly trivial, observation is the beginning of a new development which links in a significant way number theory on the one hand and probability theory on the other."

M. Kac, Statistical Independence in Probability, Analysis and Number Theory. (Wiley, 1959)

P. Erdös and M. Kac, "The Gaussian law of errors in the theory of additive number theoretic functions", American Journal of Mathematics 62 (1940) 738-742

The significant consequence of the general result is that the numbers of prime factors of large integers (suitably normalised) tend to follow the Gaussian distribution. This is stated more precisely on p.738 of the original article, but there have since been clearer reformulations of the theorem. The clearest I have found is in Kac's 1959 book.

We start with the Hardy-Ramanujan theorem (1917), which deals with numbers of prime factors of large integers:

According to Kac, the theorem states that

"Almost every integer m has approximately log log m prime factors."

More precisely, Kac explains on p.73, that Hardy and Ramanujan proved the following:

If l_n denotes the number of integers m in {1,...,n} whose number of prime factors v(m) satisfies either

then

He reproduces a proof of P. Turan, simpler than the original, and a direct analogue of the proof of the weak law of large numbers given earlier in the book.

Note that the inequalities above can be rewritten in terms of the quantity

[v(m) - log log m]/[log log m]^1/2

From Kac's book:

"5. The normal law in number theory. The fact that... the number of prime divisors of m, is the sum...of independent functions suggests that, in some sense the distribution of [its] values may be given by the normal law. This is indeed the case..."

Erdös and Kac proved the following:

Let K_n(w₁,w₂) be the number of integers m in the set {1,...,n}, for which

w₁ < [v(m) - log log n]/[log log n]^1/2 < w₂

Incidentally, the general result in the original paper concerns a general additive number theoretical function f, i.e. one which satisfies

The particular result of interest concerns f(p^k) = 1, that is, a function f which counts numbers of distinct prime factors of positive integers.

The only probabilistic component in the proof is Lemma 1, which requires the application of the Central Limit Theorem.

The authors claim Lemma 2 is the "deep" part of the proof and that Lemma 1 is "relatively superficial". But Lemma 1 is the one which concerns us here, as it involves "the central limit theorem of the calculus of probability".

We reproduce Lemma 1 and its proof here, but with the general f replaced by f(p^k) = 1, which is all we need for the particular result which interests us here. Other minor adjustments have also been made for the sake of clarity:

Lemma 1. Let f_l(m) denote the number of distinct prime factors of m which are less than l.

Denote by d_l the density of the set of integers m for which

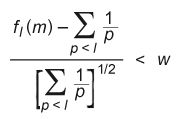
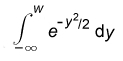
Proof: Let r_p(n) be 0 or 1 according to whether p is not or is a factor of n, then

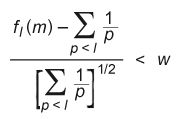
It is easy to see that the "central limit theorem of the calculus of probability" can be applied to the present case, and this proves our lemma.

The sum of a large number of independent, identically distributed variables will distribute Normally (in limit) regardless of the underlying distribution.

"The central limit theorem explains why many distributions tend to be close to the normal distribution. The key ingredient is that the random variable being observed should be the sum or mean of many independent identically distributed random variables."
 

The amazing and counterintuitive thing about the CLT is that no matter what the shape of the original distribution, the sampling distribution of the mean approaches a normal distribution. Furthermore, for most distributions, a normal distribution is approached very quickly as N increases. Keep in mind that N is the sample size for each mean and not the number of samples. Remember in a sampling distribution the number of samples is assumed to be infinite. The sample size is the number of scores in each sample; it is the number of scores that goes into the computation of each mean."
 

"The CLT and the law of large numbers are the two fundamental theorems of probability. Roughly, the CLT states that the distribution of the sum of a large number of independent, identically distributed variables will be approximately normal, regardless of the underlying distribution. The importance of the CLT is hard to overstate; indeed it is the reason that many statistical procedures work.

Ultimately, the proof hinges on a generalization of a famous limit from calculus." (from C. Stanton's online notes)
 

"I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the 'Law of Frequency of Error.' (Central Limit Theorem) The law would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement, amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. Whenever a large sample of chaotic elements are taken in hand and marshaled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along."

Francis Galton

Here is a simulation of the quincunx (or "bean machine"), a device invented by Galton to demonstrate the CLT. Here is another.

Useful references:

P. Erdös and A. Wintner, "Additive arithmetic functions and statistical independence", American Journal of Mathematical 61 (1939) 713-722.

P. Erdös, "Note on the prime divisors of integers", Journal of the London Mathematical Society 12 (1937) 308-314.

P. Hartman, E.R. van Kampen and A. Wintner, "Asymptotic distributions and statistical independence", American Journal of Mathematics 61 (1939) 477-486.

M. Kac, "Probability methods in some problems of analysis and number theory", Bulletin of the AMS 55 (1949) 641-665.

I.P. Kubilius, "Probability methods in number theory" (in Russian), Usp. Mat. Nauk 68 (1956) 31-66.

A. Renyi, "On the density of certain sequences of integers", Publ. Inst. Math. Belgrade 8 (1955) 157-162.

A. Renyi and P. Turan, "On a theorem of Erdös-Kac", Acta. Arith. 4 (1958) 71-84.

F. Saidak, "On non-abelian generalizations of the Erdös-Kac theorem and a conjecture of Erdös and Pomerance" (Ph.D. thesis summary)