
prime numbers: FAQ and resources
- What is a prime number?
- Is 1 considered to be a prime number?
- How can you tell if a number is prime or not?
- 2 is the only even prime number – why is that?
- What about 0?
- What about negative numbers?
- What are the first few prime numbers?
- Is there a formula for finding prime numbers?
- Is there a pattern in the prime numbers?
- Is there a largest prime number?
- What are twin primes?
- Why are prime numbers important?
- Why are they called "prime" numbers?
- Do prime numbers show up in the natural world?
- Is it true that prime numbers have been used in attempts to communicate with extra-terrestrials?
- How are prime numbers used in cryptography?
- Why do people search for large prime numbers?
- Do you get different prime numbers if you switch from base-10 to another base for representing numbers?
- What is the Prime Number Theorem?
- What do we know about the gaps between consecutive primes numbers?
- What is the Riemann Hypothesis?
- What's this about a link between prime numbers and quantum physics?
- Are prime numbers involved in any other areas of physics?
- What are p-adic numbers?
- 2 is the only even prime number – why is that?
further resources
- What is a prime number?
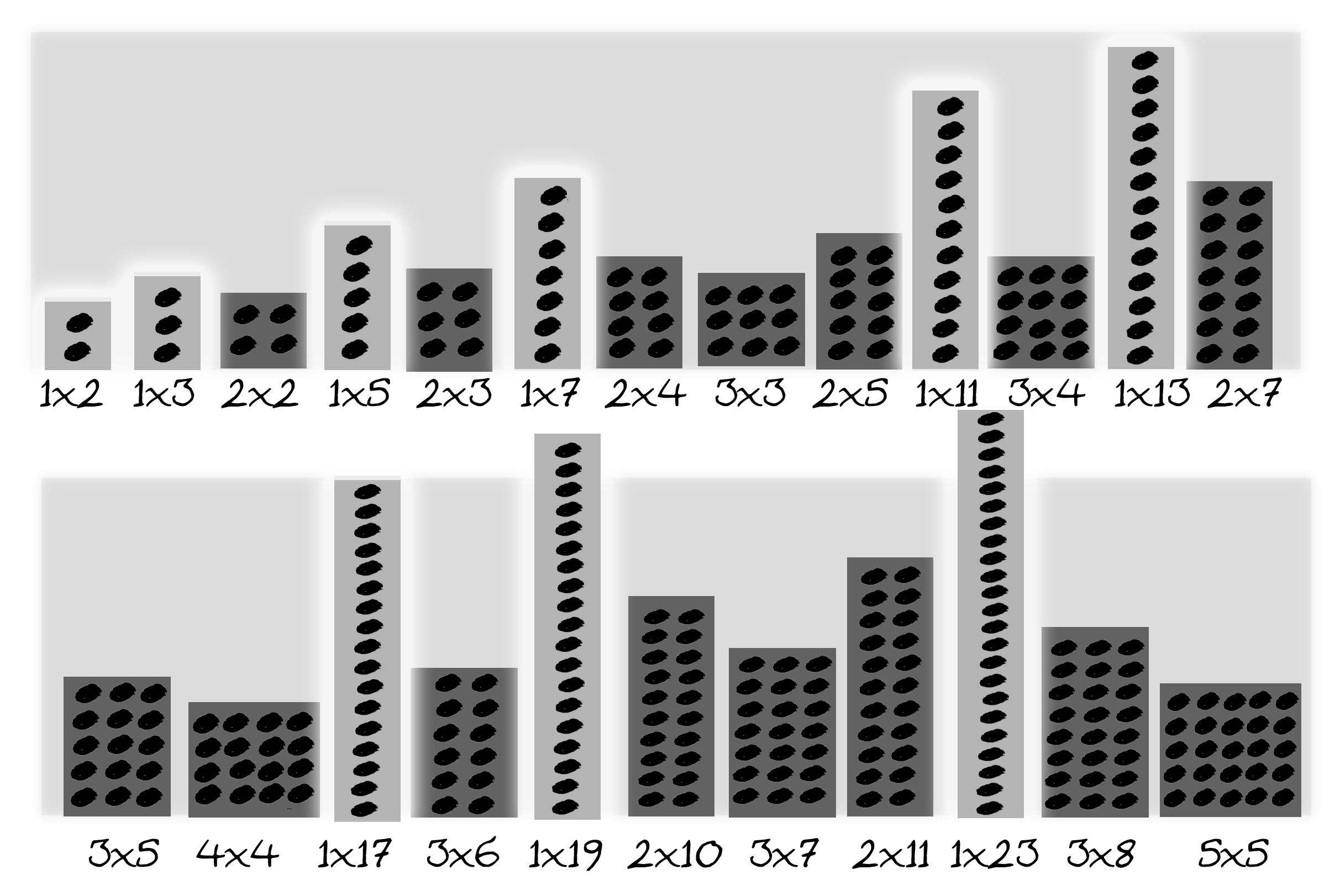
First, we'll agree that by counting numbers we mean the familar positive whole numbers 1, 2, 3, 4, 5, 6,... A prime number is a counting number which can't be divided, except by 1 or itself (every counting number can be divided by 1 and itself). That's the definition usually taught in schools. A more intuitive way of grasping what a prime number is involves trying to arrange a number of stones (or beans, or whatever) into a rectangular grid. Eight stones can be arranged in a 2×4 grid, nine stones in a 3×3 grid, ten stones in a 2×5 grid, but eleven stones cannot be arranged in a rectangular grid (a 1×11 grid doesn't count as "rectangular", otherwise this explanation would be pointless). So 8, 9 and 10 are not prime, but 11 is.
- Is 1 considered to be a prime number?
From the definition/explanation above, you wouldn't be able to tell. After all, 1 is only divisible by 1 and itself (which are the same thing!). On the other hand, one stone can't be arranged in a "rectangular grid" as I described above. It turns out that 1 is now considered not to be a prime number, but up until the late 1800s it generally was. Having hugely expanded their understanding of the number system, many good reasons emerged why we should not consider 1 to be in the same category as 2, 3, 5, 7, 11, 13, ... One of these will be mentioned below. Despite this, some people still feel driven to dispute the assertion that "1 is not a prime number". These tend to be mathematical enthusiasts presenting elaborate arguments on webpages rather than professional mathematicians contributing to the academic literature. I've even seen one argument invoking the Old Testament to "prove" that 1 is a prime! But, ultimately, like arguing about whether or not something is "art", it comes down to the definition of a word.
One way of avoiding problems with 1 in the definition of prime numbers is to define a prime to be any counting number that is divisible by exactly two counting numbers (which will be 1 and the number itself), because 1 is then excluded, only being divisible by one number (itself). Equivalently, a prime is a counting number which cannot be obtained by multiplying two smaller counting numbers.
- How can you tell if a number is prime or not?
The most straightforward way is to check all smaller counting numbers (after 1) to see if it divides by them. If not, it's prime. 29 isn't divisible by any of 2, 3, 4, ..., 28, so it's prime. In practice, there are many shortcuts: for example, if a number bigger than 2 is even then it isn't prime, and if a number bigger than 5 ends with the digit 0 or 5 then it isn't prime. And in the case of 29, we'd only need to check divisibility of numbers up to 5 (the largest counting number less than the square root of 29).
Regardless of any shortcuts, though, as counting numbers get larger, checking them for "primeness" tends to take longer. This is why finding new, ever-larger primes requires such huge computational resources.
- 2 is the only even prime number – why is that?
People sometimes dwell on this fact, but there's really nothing remarkable about it. We just happen to have a word in our language ("even") which, when applied to a counting number, means can be divided into two equal whole number amounts. All even numbers larger than 2 (that is, 4, 6, 8, 10, 12, ...) can be divided by 2 – that's what makes them even! And because they're divisible by 2 – you can divide them into two equal piles – they can't be prime numbers. 2 is even, but it's only divisible into two equal "piles of one" and you'll remember that this doesn't count, so 2 is prime.
If we invented the word treven to mean "can be divided into 3 equal whole number amounts", then 3, 6, 9, 12, 15,... would all be "treven numbers" and 3 would be the only "treven prime". For some reason, though, we have no such a word. But there's nothing to stop us inventing similar words for 5, 7, 11 or any of the other primes.
- What about 0?
Prime numbers are defined to be a class of counting numbers (1, 2, 3, 4, 5, ...), so by definition zero is excluded. In any case, 0 can be divided by any counting number (0 divided by 42 is 0 since 42×0 = 0), so there's no sense in which we can think of it as prime.
- What about negative numbers?
As with 0, negative numbers are excluded from being prime by definition. We could choose to extend our definition to include negative whole numbers, but nothing new or interesting would emerge (that is, we would end up with –2, –3, –5 –7, –11, ... , mirroring the familiar "positive primes").
- What are the first few prime numbers?
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, ... Lists of the first 1000, 10,000 and 100,000 primes are linked below.
- Is there a formula for finding prime numbers?
Not in the sense that you probably mean. It depends what you mean by "formula". There is a systematic procedure for finding primes, called the Sieve of Eratosthenes, but it's nothing like a symbolic formula that can be readily applied. The larger the numbers involved, the longer the Sieve takes. The irregularity of the primes (which are what's left over when you remove all multiples of 2, 3, 4, 5, ...) defies any kind of obvious pattern or formula. Having said that, there are some rather contrived and ultimately useless "formulas" for prime numbers collected in Appendix 4 of my book The Mystery of the Prime Numbers.
- Is there a pattern in the prime numbers?
That depends what you mean by "pattern". The simple answer is "no". In a sense, the primes are what's left over when you remove all repeating patterns from the counting numbers, so they express a kind of patternlessness. Although professional mathematicians came to accept this long ago, there's been a steady stream of poorly informed amateurs trying to "find the pattern" in the primes. More on this matter can be found in Chapter 8 of my book The Mystery of the Prime Numbers.
- Is there a largest prime number?
No. Around 300BCE, Euclid proved that the list of prime numbers goes on forever. His proof is just as valid today as it was then, and is still taught as part of undergraduate mathematics courses. It's a good example of a "proof by contradiction". You start by assuming that there is a largest prime, then you deduce a logical contradiction, proving that your assumption must be wrong. More on Euclid's theorem can be found here, and an accessible video explanation is available here.
Of course, at any given time, there's a largest prime number that we know about. As of 2016, it's 274207281–1, that is, the number you get if you multiply 2's together 74,207,281 times and then subtract 1. I've written it like that because written out fully it would have over 22 million digits! Primes of the form 2n–1 are called Mersenne primes and are generally easier to find than other types, so the ten largest primes we know about (as of early 2015) are all Mersennes. The list is available here.
- What are twin primes?
The only two primes which are directly adjacent are 2 and 3. Because there are no even primes after 2, the closest any two primes can be is two numbers apart, such as 3 and 5, 11 and 13, 29 and 31,... Such pairs are called twin primes. Although widely believed to be true, the Twin Prime Conjecture which proposes that there are infinitely many twin primes, remains one of the major unproven statements in prime number theory.
- Why are prime numbers important?
Are they important? Why is anything important? It depends on how you look at things. In most peoples' lives, prime numbers are not particularly important (only really surfacing when a group of people try to share equally a prime number of something). Less obviously, they are becoming increasingly involved in cryptography, and that affects Internet privacy, financial transactions, etc. (more below on that), so they're indirectly "important" in that sense. Within mathematics, though, prime numbers are hugely important. They effectively act as the "skeleton" of the number system, or its "building blocks". This is because of something called the the Fundamental Theorem of Arithmetic. The FTA tells us that every counting number after 1 is either a prime number, or can be "built" by multiplying prime numbers together in a unique way.
So 2 and 3 are prime, 4=2×2, 5 is prime, 6=2×3, 7 is prime, 8=2×2x×2, 9=3×3, 10=2×5, 11 is prime, 12=2×2×3, 13 is prime, 14 = 2×7, 15=3×5, 16=2×2×2×2, 17 is prime, 18=2×3×3, 19 is prime,... The numbers which aren't prime here are called composite, in that they can be "composed" of prime numbers called "prime factors". Note that the "uniqueness" of how we compose these numbers from primes does not involve the order of multiplication. For example 60 = 2×2×3×5, but it's also 2×3×2×5, 3×2×5×2, 5×2×2×3, etc., these all being different ways of expressing the same "recipe". Finding the prime factors of a counting number is called factorisation.
Incidentally, 1 is considered to be neither prime nor composite. It's clearly not composite, and if it were considered prime then the all-important FTA would no longer work (because, for example, 5 = 1×5 = 1×1×5 = 1×1×1×5 = ... so the "uniqueness of recipes" breaks down). The counting numbers can be separated out into three classes: primes, composites and "the unit" (as 1 is known in certain mathematical contexts)
More on these matters can be found in Chapter 4 of my book The Mystery of the Prime Numbers.
- Why are they called "prime" numbers?
They're "prime" in the sense that they "come first", in that we can get all of the others (composite numbers) by combining them through multiplication. When Euclid first wrote about them in his Elements, he used the Greek word "πρωτος" ("protos"), early translations of which were given as "prime", the word that has been used ever since.
- Do prime numbers show up in the natural world?
Surprisingly rarely, for such mathematically fundamental entities. As you may know, the natural world is full of mathematical patterns, but rarely ones involving prime numbers. The most widely cited example involves the 13- and 17-year life cycles of cicadas which, it is hypothesised, have evolved so that the cicadas avoid predatory species "locking into phase" with their life cycles. Here's an article about that.

- Is it true that prime numbers have been used in attempts to communicate with extraterrestrials?
Almost. In 1941, James Jeans, a physicist, astronomer and mathematician, suggested that we could bring ourselves to the attention of intelligent lifeforms on Mars, "if any such there be", by using powerful beams of light to flash, in sequence, the first prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ... when the planet was at its closest to Earth. These days, more ambitious schemes set their sights much farther than Mars and use not beams of light but extremely powerful radio signals. In 1974, a "message" was sent out from a radio telescope in Arecibo, Puero Rico, involving a repeating string of 1,679 binary digits (0's and 1's). The hope was that any intelligent recipient would recognise that 1679 = 23×73 (1679 is composite and this is its unique "prime decomposition"). Converting the 1679 binary digits into a rectangular grid involving 73 rows of 23 black or white squares then reveals a crude block diagram showing some basic facts about humans' biological makeup, Earth's position in the solar system, etc. Here is more on the "Arecibo message". Chapter 5 of my book The Mystery of the Prime Numbers deals with prime numbers and extraterrestrial communication.

- How are prime numbers used in cryptography?
There's an encryption method known as RSA (first described by Rivest, Shamir and Adelman in 1977) which involves using a pair of large prime numbers to encrypt and decrypt messages. A user makes one such prime number known as their "public key" and keeps the other secret as their "private key". If I wanted to send you an RSA-encrypted message, I would use a piece of software that uses your public key to scramble the original text. For anyone who intercepts this message to decrypt it, they would need your private key. The RSA method works because of the fact that while it's relatively easy (with a computer) to multiply two (say) 300-digit prime numbers, to work out what those primes were from the resulting (roughly) 600-digit product would require more computing power than is currently available on the planet. Very simply, it's quite easy to multiply two large counting numbers, but "factorising" the result is very, very difficult. An accessible video explaining how RSA works is available here. A more detailed (and more technical) explanation can be found here.
- Why do people search for large prime numbers?
Although prime numbers of a certain size are useful as "keys" in the application of RSA encryption (see previous question), the large primes that some people dedicate their time to searching for (using computer algorithms) are of little mathematical interest. After all, we know that the primes continue to appear forever (that is, there's no largest prime number) so the idea of a "large" prime is always relative to human concepts of what constitutes a "large" number. The motivation for seeking the largest prime number yet found by humans is comparable to the motivation for attempting to climb mountains, break athletic records or otherwise make one's mark in the world in a way which involves comparative quantities (more metres of altitude, less seconds of clock time, etc.) It's the kind of mentality which is responsible for the ongoing popularity of the Guiness Book of World Records.
In recent years, distributed computation has been enlisted in the search for ever larger primes, with projects like the Great Internet Mersenne Prime Search recruiting members of the public who install some software which links their Internet-connected computer to a network of others when its processor is otherwise idle. In this way, the huge computational task of testing ever-larger numbers for primality is divided up between tens of thousands of computers all cooperating via the centralised control of the GIMPS server. The top ten largest known primes were all discovered by the GIMPS project between 2001 and 2013.
Chris Caldwell explores the various reasons why people seek large primes here.
- Do you get different prime numbers if you switch from base-10 to another base for representing numbers?
No. It doesn't matter if you represent your numbers in base-10, base-12, binary, Roman numerals or Mayan glyphs, if you have twenty-three pebbles, there's no way of dividing them into a number of equal-sized piles (or equivalently arranging them in a rectangular grid). The representation of counting numbers has no bearing on their mathematical properties such as whether they are prime or composite.

- What is the Prime Number Theorem?
The Prime Number Theorem was first suggested at the end of 18th century, and eventually proved at the end of the 19th. It describes how the prime numbers tend to "thin out" as we proceed through the counting numbers, involving a kind of "approximate" formula. This formula tells us that the number of primes less than a given number n can be roughly approximated by dividing n by its own natural logarithm. A simple, geometric way of thinking about natural logarithms involves the following figure:

To find the natural logarithm of 258, we imagine circles of radius 1 and 258 centred at the centre of the spiral (a very particular example of an equiangular spiral, the kind you see in seashells and snailshells). We then count the number of coils of the spiral enclosed between those two circles. In the example above, although the circle of radius 1 is too small to see, the number of coils is 5.553..., so we say that the natural logarithm of 258 (written either "ln 258" or "log 258") is 5.553... Hence the Prime Number Theorem tells us that there are roughly 258 ÷ 5.553... or 46.462... primes less than 258. In actuality, it's 55. That's an accuracy of about 84% – not terribly good – but by considering sufficiently large counting numbers, this accuracy can be proven to get as close to 100% as you require.
More on the Prime Number Theorem can be found here, or in Chapter 10 of my book The Mystery of the Prime Numbers.
- What do we know about the gaps between consecutive primes numbers?
From the Prime Number Theorem (see previous question), it's possible to deduce that the average gap between primes less than a given number n is approximately the natural logarithm of n, and as with the PNT, this approximation becomes as accurate as you would like if you consider sufficiently large numbers n. A lot of work has been done on "record" gaps and bounds on the sizes of gaps. In 2013, Yitang Zhang of the University of New Hampshire published a widely acclaimed paper which provide the first finite bound on prime gaps. More information on prime gaps can be found here.
- What is the Riemann Hypothesis?
The Riemann Hypothesis is arguably the most famous unsolved problem in mathematics, named after the German mathematician Bernhard Riemann who first proposed it in 1859. Because it is intimately connected to so many other areas of mathematics, it's often refered to as the "Holy Grail of mathematics". To understand it requires a familiary with quite a lot of higher mathematics (complex number, functions of a complex variable, analytic continuation, etc.), so a simple explanation can't be given here, but more information can be gleaned from my Riemann Hypothesis FAQ and resources page.
It arose from Riemann's investigation of the "prime counting function" which keeps track of how many primes occur less than a given number, so it's closely related to the prime numbers, although in the form it's usually stated (something like "All non-trivial zeros of the Riemann zeta function have real part 1/2.") that's not immediately obvious. The "Riemann zeta function" is a function on the complex plane whose "non-trivial zeros" in some sense control the fluctuations in the distribution of prime numbers. One somewhat over-simplified way of summarising the RH is to say that if it's true, then the prime numbers are as "well behaved as possible", or that they're "as random as possible" given the constraint that the Fundamental Theorem of Arithmetic (see above) must work. If the RH turns out to be false then there would be huge fluctuations in the distribution of primes, disrupting a certain balance within the number system. With very few exceptions, the mathematical community tends to believe (and hope) that it's true.
Since the nonprofit Clay Mathematics Foundation offered a $1,000,000 prize for a proof of the RH in 2000, there has been considerable popular interest in the problem. This led to several books aimed at a popular audience, including du Sautoy's The Music of the Primes, Derbyshire's Prime Obsession and Sabbagh's Dr. Riemann's Zeros (all published in 2003). An outline of the main issues relating to the RH can be found here. An in-depth and visually-oriented exploration, which requires no background in higher mathematics, can be found in my Secrets of Creation trilogy.
- What's this about a link between prime numbers and quantum physics?
To understand this requires a familiarity with quantum physics, chaos theory and the Riemann zeta function, so the best I can do here is to give a very sketchy outline. Part of Riemann's work on the distribution of primes showed that the "prime counting function" can be understood in terms of a set of wave-like mathematical objects. As with waves in physics, these have wavelengths and frequencies. There's an infinite number of them and their frequencies collectively make up what's called a "spectrum". In the early 1980s, the physicist Michael Berry noticed that this spectrum corresponds remarkably closely to the spectrum associated with a type of physical oscillating system.
Although it's very common to find mathematical structures reflected in physical reality (this is the basis of modern physics), this is a very strange reversal of that situation, where a physical structure is mirrored in mathematical reality. A very specific class of "quantum chaological" oscillators appears to somehow underlie the distribution of prime numbers (and thereby the system of counting numbers). No one knows what this means, and it's the strangest thing I'm aware of in my experience of reality! This is all patiently explained (without any prerequisite maths or physics) in the final volume of my Secrets of Creation trilogy.
- Are prime numbers involved in any other areas of physics?
Yes, they're involved in many diverse areas of physics (either directly, or via the related Riemann zeta function). Most of these connections were discovered in the 20th century, and were generally accompanied with surprise, as number theory (which is concerned just with the properties of the counting numbers) is the last area of maths you would expect to be relevant to physics. I've been collecting research materials linking number theory and physics for my online number theory and physics archive since the late 1990s, and the overall feeling these engender is not far from the mystical Pythagorean motto "all is number".
- What are p-adic numbers?
The rational numbers (all the positive and negative ratios of counting numbers) form a dense continuum on the number line, but not a "closed set". Effectively there are "holes", like the well-known irrational numbers π, e, √2 and φ (the golden mean). There are in fact infinitely many such "holes", and the most familiar way to "fill them in" is to "complete" the rational numbers in order to arrive at the continuum real numbers, which include all rational and irrational numbers, a closed set.
However, in the 1890s it was discovered that there are infinitely many other ways to "complete" the set of rational numbers, and each of these produces a radically different number system. There turns out to be one for each prime number, and they've become known as the 2-adic, 3-adic, 5-adic, 7-adic, etc. number systems. They key is to change the way you define the distance between two rational numbers. The familiar way is to subtract the smaller number from the larger, to get the kind of distance associated with conventional measurement. The "p-adic" approach (where p stands for an arbitrary prime) involves looking at that same difference (a rational number, assumed to be in reduced fraction form) and then the power of p that appears in its numerator or denominator. In this way, two rational numbers which might be considered "nearby" in the real number system can be vast distances apart in a p-adic system (and vice versa).
A more detailed explanation of p-adic numbers can be found here.
- Is 1 considered to be a prime number?
List of the first 10,000 primes
List of the first 100,000 primes
the distribution of prime numbers (elementary, visually-oriented presentation)
the Sieve of Eratosthenes (for kids of all ages)
quotations about the mysterious qualities of the prime distribution
the prime number theorem (proof outline and additional notes)
the Riemann Hypothesis FAQ and resources
Riemann's zeta function resources
D. Rockmore, "Chance in the Primes" [part 1] [part 2] [part 3]
This excellent and thorough article is intended as a commentary to supplement the first half of a popular talk on
the Riemann Hypothesis given by Peter Sarnak at a 1998 MSRI conference (a video recording of which
is available here).
how the complex zeros of Riemann's zeta function "encode" the distribution of primes
the functional equation of the Riemann zeta function and related issues
D. Bump's lecture notes on the distribution of the Riemann zeta function's nontrivial zeros
summary of Ilan Vardi's (excellent) "Introduction to Analytic Number Theory"
mystery new number theory and physics archive search home