a sum of coefficients can be expressed in terms of a contour integral:

The mark above the summation symbol on the left-hand side means that the step function in question is modified so that at points of discontinuity, it takes a value halfway between its limits on either side (this phenomenon is familiar in the theory of Fourier analysis).

The value c must be positive, and greater than some u where the series f(s) is convergent for s = u + iv. There is an elementary theorem on Dirichlet series which guarantees that if f is convergent for s = u + iv, then it's convergent for any value of s whose real part is greater than u (see Theorem 1, Hardy and Riesz).

A proof of Perron's formula can be found in Hardy and Riesz (Theorem 13). This involves a limit of expanding rectangular contours whose left edges lie on the vertical line Re[s] = c.

We shall now apply Perron's formula to the particular case of the Dirichlet series .

[Note that it must first be established that this equation can be extended so that it becomes valid for a complex variable s rather than just a real variable x.]

If we take and , then , so that

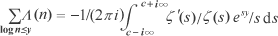
A change of variables where x = e^y gives (for c > 1)

The inclusion of the subscript in indicates the modification of which was mentioned above. That is, at those values of x where there is a step (discontinuity), the average value is interpolated.