GECO: Dynamics of Phase Oscillator Networks with Generalized Coupling Marie Curie Intra-European Fellowship (FP7-PEOPLE-2013-IEF, Project No. 626111) Fellow: Christian Bick Host: Peter Ashwin Institution: University of Exeter, United Kingdom Period: January 2015–August 2017

Overview

The interaction of units which undergo repetitive motion is one of the fundamental schemes in nature and technology. For example these oscillations are crucial to make our hearts beat: all heart cells have to contract together at the same time. Typically, the interaction between units is assumed to be simple whereas more complicated interaction has been neglected.

Understanding the dynamics of oscillatory units with complicated interaction is the main goal of GECO: what are the features of networks of coupled oscillators with generalized coupling? Of particular interest symmetric and near-symmetric systems. The understanding of these dynamical phenomena goes well beyond the results in the current literature. More specifically, GECO addresses a number of specific research questions. Why and how does degeneracy found in finite collections of oscillators for simple coupling disappear when one makes the interaction more complicated? If one allows the number of oscillators to be infinite, what dynamics are possible in this "continuum limit"? Are there any genuinely new dynamics that may emerge through more complicated coupling? Answering these questions will explore new ground in the study of coupled oscillators and may consolidate existing results and put them into perspective.

Events

Projects

Dynamics of Small Networks with Full Symmetry

To study the onset of synchronization, Kuramoto introduced his seminal model of coupled phase oscillators. In his setup, the interaction between individual units is given by the sine of their relative phases. For this particular interaction function and identical oscillators, the dynamics of globally, identically coupled oscillators are degenerate. However, higher order harmonics in the interaction function or nonpairwise interaction terms arise quite naturally in many systems. We found that such networks with generalized coupling can give rise to interesting nontrivial dynamics such as chaos.

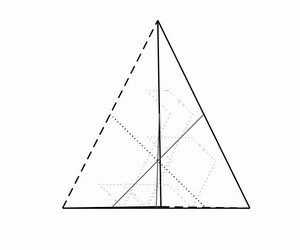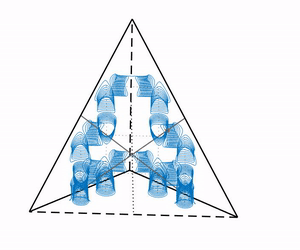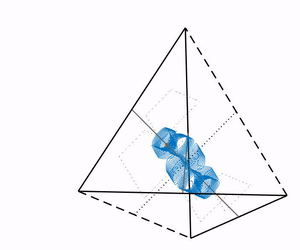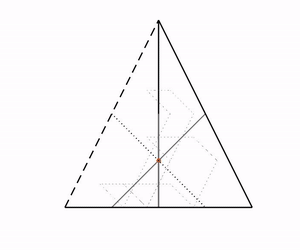
To understand how such complicated dynamics arise we study for example the bifurcations of these systems. For systems with pairwise coupling the dynamics are particularly rich for coupling functions that are close to even. Even coupling induces an additional time-reversing symmetry which gives rise to periodic orbits for 4 oscillators (shown in the animation to the right). For generic symmetrically coupled systems higher order, nonpairwise interaction terms can induce chaos.

Results and Publications

• Christian Bick, Peter Ashwin, and Ana Rodrigues. Chaos in generically coupled phase oscillator networks with nonpairwise interactions. [ Article ].
• Peter Ashwin, Christian Bick, and Oleksandr Burylko. Identical Phase Oscillator Networks: Bifurcations, Symmetry and Reversibility for Generalized Coupling. [ Article ].

Localized Collective Dynamics in Small Networks

The emergence of collective dynamics is a fascinating effect in coupled oscillatory systems. In particular the emergence of localized synchrony, solutions commonly know as chimera states, have attracted attention in recent years. The notion of a weak chimera yields a mathematically rigorous definition of a chimera state in terms of frequency synchrony—breaking full symmetry is a prerequisite to observe such dynamics. Here we explore the existence of weak chimeras and study how generalized coupling can generate chaotic dynamics. Moreover, we relate weak chimeras to the symmetries of a network of identical oscillators: if two oscillators are frequency synchronized, the collection of frequencies is invariant under the permutation that swaps the oscillators.

Localized frequency synchrony, weak chimeras, can be observed in a network of electrochemical oscillators. The animation to the right shows experimental data from a setup of four oscillators, the blue population is in an anti-phase (splay) configuration, the red population is approximately in phase. The oscillators within each population have the same average frequency while the populations rotate relative to each other.

Results and Publications

• Christian Bick and Peter Ashwin. Chaotic Weak Chimeras and their Persistence in Coupled Populations of Phase Oscillators. [ Article ].
• Christian Bick. Isotropy of angular frequencies and weak chimeras with broken symmetry. [ Article ].
• Christian Bick, Michael Sebek, and István Z. Kiss. Robust Weak Chimeras in Oscillator Networks with Delayed Linear and Quadratic Interactions. [ Article ].

Dynamics of Large Networks

A natural setup to study coherence-incoherence patterns in large networks are networks that consist of multiple interacting populations. We generalize the coupling to account for heterogeneous phase lag parameters which can occur for example to approximate distributed transmission delays in applications. In contrast to networks with identical phase lag, we find that such networks not only support chimera states but also chaotic dynamics.

Results and Publications

• Erik A. Martens, Christian Bick, and Mark J. Panaggio. Chimera States in Two Populations with Heterogeneous Phase Lag. [ Article ].

Nonsmooth Generalized Coupling

Real-world networks often have inherently nonsmooth dynamics: nodes may stop and restart at some time, connections between nodes may vary. This includes networks made up of oscillatory units such as rotator models that have recently been used to study the dynamics of power grids. Switching of network connectivity and other nonsmooth effects that arise in the study of such asynchronous oscillatory networks constitute an important for of generalized coupling as they go beyond the classical smooth phase oscillator models.

Results and Publications

• Christian Bick and Michael Field. Functional Asynchronous Networks: Factorization of Dynamics and Function. [ Article ].
• Christian Bick and Michael Field. Asynchronous networks and event driven dynamics. [ Article ].
• Christian Bick and Michael Field. Asynchronous networks: modularization of dynamics theorem. [ Article ].

Communication

1. Universidade de Santiago de Compostela, Santiago de Compostela, Spain (Oct 2016)
2. Universitat Pompeu Fabra, Barcelona, Spain (Oct 2016)
3. Vrije Universiteit Amsterdam, Amsterdam, The Netherlands (June 2016)
4. Loughborough University, Loughborough, United Kingdom (May 2016)
5. University of Manchester, Manchester, United Kingdom (May 2016)
6. University of Bristol, Bristol, United Kingdom (Feb 2016)
7. University of Edinburgh, Edinburgh, United Kingdom (Feb 2016)
8. Technische Universität Berlin, Berlin, Germany (Jan 2016)
9. Washington University in St. Louis, St. Louis, Missouri, United States (Dec 2015)
10. Ochanomizu University, Tokyo, Japan (Oct 2015)
11. RIKEN Brain Sciences Institute, Saitama, Japan (Oct 2015)
12. Osaka Prefecture University, Osaka, Japan (Oct 2015)
13. Brigham Young University, Provo, Utah, United States (May 2015)
14. Imperial College, London, United Kingdom (April 2015)
15. Universität Hamburg, Hamburg, Germany (April 2015)

Contact

Christian Bick
College of Engineering, Mathematics and Physical Sciences
University of Exeter
Harrison Building
North Park Road
Exeter EX4 4QF
United Kingdom