



Next: Further sources of information
Up: Introduction to time series
Previous: Serial correlation
Contents
Auto-Regressive Integrated Moving Average (ARIMA) time series
models form a general class of linear models that are
widely used in modelling and forecasting time series
(Box and Jenkins, 1976). The ARIMA(p,d,q) model of the time
series
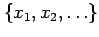 is defined as
is defined as
where 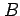 is the backward shift operator,
is the backward shift operator,
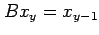 ,
,
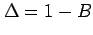 is the backward difference, and
is the backward difference, and
 and
and  are polynomials of order
are polynomials of order
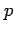 and
and 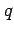 , respectively.
ARIMA(p,d,q) models are the product of an
autoregressive part AR(p)
, respectively.
ARIMA(p,d,q) models are the product of an
autoregressive part AR(p)
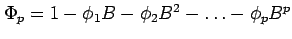 ,
an integrating part
,
an integrating part
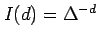 , and
a moving average MA(q) part
, and
a moving average MA(q) part
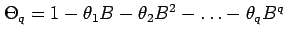 .
The parameters in
.
The parameters in 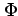 and
and 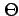 are chosen so that
the zeros of both polynomials lie outside the unit circle
in order to avoid generating unbounded processes.
The difference operator takes care of ``unit root''
are chosen so that
the zeros of both polynomials lie outside the unit circle
in order to avoid generating unbounded processes.
The difference operator takes care of ``unit root'' 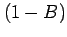 behaviour in the time series and for
behaviour in the time series and for 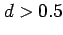 produces non-stationary
behaviour (e.g. increasing variance for longer time series).
produces non-stationary
behaviour (e.g. increasing variance for longer time series).
An example of an ARIMA model is provided by the ARIMA(1,0,0)
first order autoregressive model
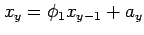 . This simple
AR(1) model has often been used as a simple ``red noise'' model
for natural climate variability.
. This simple
AR(1) model has often been used as a simple ``red noise'' model
for natural climate variability.




Next: Further sources of information
Up: Introduction to time series
Previous: Serial correlation
Contents
David Stephenson
2005-09-30
![]() . This simple
AR(1) model has often been used as a simple ``red noise'' model
for natural climate variability.
. This simple
AR(1) model has often been used as a simple ``red noise'' model
for natural climate variability.