We are often interested in the case when two events happen at the same
time. For example, to get snow falling on the ground, it is necessary
that two events, ![]() =``precipitating cloud''} and
=``precipitating cloud''} and
![]() =``boundary layer below freezing''} occur at the same time.
The probability of two events happening at the same time,
=``boundary layer below freezing''} occur at the same time.
The probability of two events happening at the same time,
![]() and
and ![]() , is known as the joint probability of events
, is known as the joint probability of events
![]() and
and ![]() . For mutually exclusive events that never occur at the
same time, the joint probability is zero.
. For mutually exclusive events that never occur at the
same time, the joint probability is zero.
It is also useful to define the probability of an event GIVEN that another
event has happened. This approach is very powerful and is known as
conditioning. The conditional probability of an event ![]() given
given ![]() (i.e. conditioned on
(i.e. conditioned on ![]() ) is defined as
) is defined as
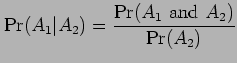 |
(3.1) |
For independent events,
![]() and
and ![]() and so the conditional probability
and so the conditional probability
![]() - in other words, conditioning on independent
events does not change the probability of the event. This is the
definition of independence.
- in other words, conditioning on independent
events does not change the probability of the event. This is the
definition of independence.
By equating
![]() and
and ![]() and
and
![]() and
and ![]() , one can derive
the following useful identity
, one can derive
the following useful identity
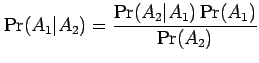 |
(3.2) |