



Next: Summary of statistical notation
Up: Basic probability concepts
Previous: Odds
Contents
If probabilities are known for all events in event space, it is
possible to calculate the expectation (population mean)
of a random variable 
where 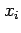 is the value taken by the random variable
is the value taken by the random variable  for event
for event
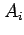 ; i.e.
; i.e.
 .
As an example, if there is a one in a thousand chance of
winning a lottery prize of £1500 and each lottery
ticket costs £2 then the expectation (expected long
term profit) is -£0.50=
.
As an example, if there is a one in a thousand chance of
winning a lottery prize of £1500 and each lottery
ticket costs £2 then the expectation (expected long
term profit) is -£0.50=
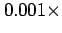 £(1500-2)
£(1500-2)
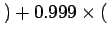 -£2
-£2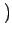 .
A useful property of expectation is that the expectation of any
linear combination of two random variables
is simply the linear combination of their respective
expecations
.
A useful property of expectation is that the expectation of any
linear combination of two random variables
is simply the linear combination of their respective
expecations
where 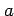 and
and 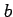 are (non-random) constants. Note also
that
are (non-random) constants. Note also
that
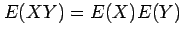 if X and Y are independent random
variables.
if X and Y are independent random
variables.
The expectation can also be used to define the population
variance
which provides a very useful measure of the overall
uncertainty in the random variable.
The variance of a linear combination of two
random variables is given by
where 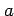 and
and 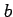 are (non-random) constants.
The quantity
are (non-random) constants.
The quantity
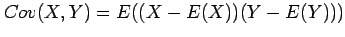 is known as the
covariance of
is known as the
covariance of  and
and 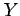 and is equal to zero
for independent variables.
The covariance can be expressed as
and is equal to zero
for independent variables.
The covariance can be expressed as
where 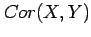 is a dimensionless number lying between -1 and 1
known as the correlation between
is a dimensionless number lying between -1 and 1
known as the correlation between  and
and 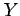 .
Correlation is widely used to measure the amount of
linear association between two variables.
.
Correlation is widely used to measure the amount of
linear association between two variables.
Note that the quantities 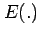 and
and 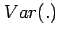 refer
specifically to population parameters and
NOT sample means and variances. To avoid confusion
the sample mean of an observed variable
refer
specifically to population parameters and
NOT sample means and variances. To avoid confusion
the sample mean of an observed variable 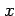 is denoted by
is denoted by
 and the sample variance is denoted by
and the sample variance is denoted by 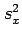 .
Sample covariance is denoted
.
Sample covariance is denoted  and sample correlation
is denoted by
and sample correlation
is denoted by  .
These provide estimates of the population quantities but
should never be confused with them !
.
These provide estimates of the population quantities but
should never be confused with them !




Next: Summary of statistical notation
Up: Basic probability concepts
Previous: Odds
Contents
David Stephenson
2005-09-30
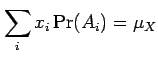
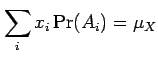
![]() and
and ![]() refer
specifically to population parameters and
NOT sample means and variances. To avoid confusion
the sample mean of an observed variable
refer
specifically to population parameters and
NOT sample means and variances. To avoid confusion
the sample mean of an observed variable ![]() is denoted by
is denoted by
![]() and the sample variance is denoted by
and the sample variance is denoted by ![]() .
Sample covariance is denoted
.
Sample covariance is denoted ![]() and sample correlation
is denoted by
and sample correlation
is denoted by ![]() .
These provide estimates of the population quantities but
should never be confused with them !
.
These provide estimates of the population quantities but
should never be confused with them !