



Next: Further reading
Up: Basic probability concepts
Previous: Expectation, (co-)variance, and correlation
Contents
Mathematical notation in statistics can often be a source
of confusion. Here is a brief summary of some commonly used
conventions:
- Upper case Roman letters are used to denote random variables
(e.g.
 ,
, 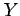 ,
, 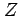 , etc.) whereas lower case Roman letters are
used to denote their specific values (e.g.
, etc.) whereas lower case Roman letters are
used to denote their specific values (e.g. 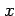 ,
, 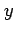 , and
, and 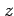 ).
For example, the probability of a (generic) random variable
).
For example, the probability of a (generic) random variable  exceeding a (specific) value
exceeding a (specific) value 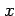 is given by
is given by
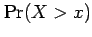 .
Therefore, sample data such as measurements are denoted by
lower case Roman letters (e.g. a data sample with values
.
Therefore, sample data such as measurements are denoted by
lower case Roman letters (e.g. a data sample with values
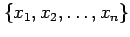 ).
).
- Unobservable quantities such as model parameters and noise
are denoted using lower case Greek letters. For example, the
linear regression model that explains random variable
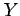 in
terms of
in
terms of  is given by
is given by
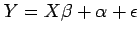 .
.
- The hat symbol is used to denote estimated and predicted values.
For example,
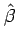 is an estimate of the model parameter
is an estimate of the model parameter
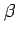 , and
, and 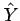 is a prediction of the random variable
is a prediction of the random variable 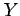 .
.
- Bold face upper case Roman letters are used to denote data matrices
containing multiple variables. For example, the
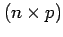 data
matrix
data
matrix 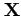 contains elements
contains elements 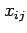 where row index
where row index
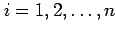 refers to the data items/objects, and column index
refers to the data items/objects, and column index
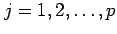 refers
to the variables.
refers
to the variables.
- The symbol
 is often used to denote the sample size (the number of
data objects in the sample).
is often used to denote the sample size (the number of
data objects in the sample).
- The population mean
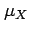 is written in terms of the expectation
operator as
is written in terms of the expectation
operator as
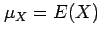 whereas the sample mean is denoted using
an overline (e.g.
whereas the sample mean is denoted using
an overline (e.g.
 ). Sometimes climate studies using
the quantum mechanics bra-ket notation
). Sometimes climate studies using
the quantum mechanics bra-ket notation 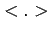 to denote expectation
but this non-standard practice should be avoided.
to denote expectation
but this non-standard practice should be avoided.




Next: Further reading
Up: Basic probability concepts
Previous: Expectation, (co-)variance, and correlation
Contents
David Stephenson
2005-09-30