



Next: Example 2: Binomial distribution
Up: Theoretical discrete distributions
Previous: Theoretical discrete distributions
Contents
A Bernoulli (binary) variable is a random variable that
can take only the value of either
1 (success) or 0 (failure).
Bernoulli variables are commonly
used for describing binary
processes such as coin tossing, rain/no rain, yes/no decisions etc..
The Bernoulli distribution uses one population parameter 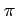 to define the probability of success
to define the probability of success
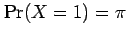 and the
probability of failure
and the
probability of failure
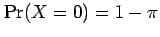 .
This can be written more succinctly as
.
This can be written more succinctly as
where 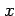 takes the value of either 0 or 1.
The parameter
takes the value of either 0 or 1.
The parameter 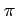 completely determines the population distribution
and all possible statistics based on
completely determines the population distribution
and all possible statistics based on  , for example, the population
mean is given by
, for example, the population
mean is given by
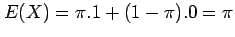 and the population variance is given
by
and the population variance is given
by
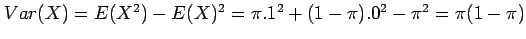 .
A random variable
.
A random variable  distributed with a Bernoulli distribution
is described as
distributed with a Bernoulli distribution
is described as
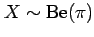 by statisticians (the
by statisticians (the 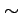 symbol
means ``distributed as'').
symbol
means ``distributed as'').
David Stephenson
2005-09-30