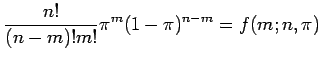Next: Example 3: Poisson distribution
Up: Theoretical discrete distributions
Previous: Example 1: Bernoulli distribution
Contents
Suppose we are interested in counting
the number of times  a Bernoulli event with
probability
a Bernoulli event with
probability 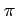 happens in a fixed number
happens in a fixed number  of independent trials.
For example, we might be interested in counting
the total number of times hurricanes hit Florida
out of a specified number of hurricane events.
The probability distribution of such a count variable
is given by the Binomial distribution
of independent trials.
For example, we might be interested in counting
the total number of times hurricanes hit Florida
out of a specified number of hurricane events.
The probability distribution of such a count variable
is given by the Binomial distribution
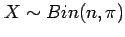 defined as
defined as
for
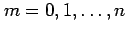 where
where
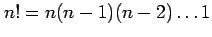 and
and 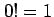 .
The fraction containing factorials on the left hand side
is the number of possible ways
.
The fraction containing factorials on the left hand side
is the number of possible ways 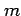 successes can happen
out of
successes can happen
out of  events, and this can often be surprisingly large.
A binomially distributed variable has expectation
events, and this can often be surprisingly large.
A binomially distributed variable has expectation
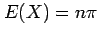 and variance
and variance
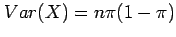 .
In the limit of large
.
In the limit of large  , the binomial distribution is
well approximated by a normal distribution with mean
, the binomial distribution is
well approximated by a normal distribution with mean
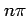 and variance
and variance
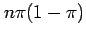 .
So for example, if the probability of a hurricane hitting
Florida is
.
So for example, if the probability of a hurricane hitting
Florida is 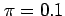 , then out of 200 hurricanes, one would
expect a mean of
, then out of 200 hurricanes, one would
expect a mean of
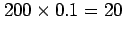 hurricanes to hit
Florida with a standard deviation of
hurricanes to hit
Florida with a standard deviation of
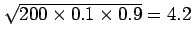 hurricanes.
The binomial distribution is useful for estimating the
fraction of binary events
hurricanes.
The binomial distribution is useful for estimating the
fraction of binary events 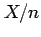 such as the fraction
of wet days, or the fraction of people voting for a
political party.
such as the fraction
of wet days, or the fraction of people voting for a
political party.




Next: Example 3: Poisson distribution
Up: Theoretical discrete distributions
Previous: Example 1: Bernoulli distribution
Contents
David Stephenson
2005-09-30
![]() a Bernoulli event with
probability
a Bernoulli event with
probability ![]() happens in a fixed number
happens in a fixed number ![]() of independent trials.
For example, we might be interested in counting
the total number of times hurricanes hit Florida
out of a specified number of hurricane events.
The probability distribution of such a count variable
is given by the Binomial distribution
of independent trials.
For example, we might be interested in counting
the total number of times hurricanes hit Florida
out of a specified number of hurricane events.
The probability distribution of such a count variable
is given by the Binomial distribution
![]() defined as
defined as