



Next: Example 4: Uniform distribution
Up: Theoretical discrete distributions
Previous: Example 2: Binomial distribution
Contents
Often we do not know the total number of trials,
but we just know that events occur independently
and not simultaneously at a mean rate of
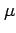 in a certain region of space or in an interval time.
For example, we might know that there are a mean number
of 20 hurricanes in the Atlantic region per year.
In such cases, the number of events
in a certain region of space or in an interval time.
For example, we might know that there are a mean number
of 20 hurricanes in the Atlantic region per year.
In such cases, the number of events  that occur in a fixed
region or time interval is given by the Poisson distribution
that occur in a fixed
region or time interval is given by the Poisson distribution
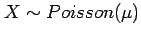 defined by
defined by
for
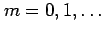 .
A Poisson distributed count variable has expectation
.
A Poisson distributed count variable has expectation
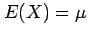 and variance
and variance
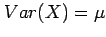 .
The Poisson distribution approximates the Binomial
distribution in the limit of large
.
The Poisson distribution approximates the Binomial
distribution in the limit of large  and finite
and finite
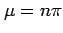 .
The sum of two independent Poisson distributed
variables is also Poisson distributed
.
The sum of two independent Poisson distributed
variables is also Poisson distributed
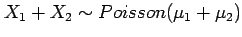 .
Meteorological events such as storms often satisfy the
independence and non-simultaneity criteria necessary
for a Poisson process and so the number of such
events in a specified region or time interval can be
satisfactorily modelled using the Poisson distribution.
.
Meteorological events such as storms often satisfy the
independence and non-simultaneity criteria necessary
for a Poisson process and so the number of such
events in a specified region or time interval can be
satisfactorily modelled using the Poisson distribution.




Next: Example 4: Uniform distribution
Up: Theoretical discrete distributions
Previous: Example 2: Binomial distribution
Contents
David Stephenson
2005-09-30

