



Next: Accuracy and bias of
Up: Parameter estimation
Previous: Example 3: Confidence Interval
Contents
Generally, a population parameter can be estimated in a variety of
different ways by using several different sample statistics.
For example, the population mean can be estimated using estimators
such as the sample mean, the sample median, and even more exotic
sample statistics such as trimmed means etc..
This raises the question of which method to use to choose the best estimator.
The three most frequently used estimation approaches are:
- Moment method - the sample moments,
 ,
,
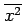 ,
,
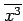 , etc., are
used to provide simple estimates of the location, scale, and
shape parameters of the population distribution. Although
these are the most intuitive choices for estimator, they have
the disadvantage of giving biased estimates for non-normal
distributions (non-robust), and can also be unduly influenced by the
presence of outliers in the sample (non-resistant).
, etc., are
used to provide simple estimates of the location, scale, and
shape parameters of the population distribution. Although
these are the most intuitive choices for estimator, they have
the disadvantage of giving biased estimates for non-normal
distributions (non-robust), and can also be unduly influenced by the
presence of outliers in the sample (non-resistant).
- Robust estimation - instead of using moments, robust estimation
methods generally
use statistics based on quantiles e.g. median, interquartile
range, L-moments, etc.. These measures are more robust and resistant
but have the disadvantage of giving estimators that have larger
sampling errors (i.e. less efficient estimators - see next section).
- Maximum Likelihood Estimation (MLE) - These are most widely used
estimators because of their many desirable properties. MLE estimates
are parameter values chosen so as to maximise the likelihood of obtaining the
data sample. In simple cases such as normally distributed data, the MLE
procedure leads to moment estimates of the mean and variance. For more
complicated cases, the MLE approach gives a clear and unambiguous approach
for choosing the best estimator.




Next: Accuracy and bias of
Up: Parameter estimation
Previous: Example 3: Confidence Interval
Contents
David Stephenson
2005-09-30