



Next: Example 1: The sample
Up: Parameter estimation
Previous: Choice of estimator
Contents
The accuracy of an estimator
 can be
evaluated by its Mean Squared Error
can be
evaluated by its Mean Squared Error
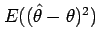 .
The MSE can be decomposed into the sum of two parts:
.
The MSE can be decomposed into the sum of two parts:
The first term is the square of the mean bias
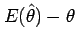 and measures the difference
the mean of ALL sample estimates and the true population
parameter.
The second term is the variance of the sample estimate caused
by sampling uncertainty due to finite sample size.
Bias can sometimes be reduced by choosing a different estimator
but often at the expense of increased variance.
and measures the difference
the mean of ALL sample estimates and the true population
parameter.
The second term is the variance of the sample estimate caused
by sampling uncertainty due to finite sample size.
Bias can sometimes be reduced by choosing a different estimator
but often at the expense of increased variance.
Estimators with smaller MSE are called more
efficient estimators, and ones with
the smallest MSE are called Least Squared Error (LSE)
estimators.
To obtain the smallest MSE, it is necessary to have small or
even no bias (unbiased) and low variance.
Subsections
David Stephenson
2005-09-30
![]() can be
evaluated by its Mean Squared Error
can be
evaluated by its Mean Squared Error
![]() .
The MSE can be decomposed into the sum of two parts:
.
The MSE can be decomposed into the sum of two parts: