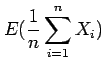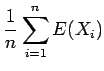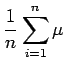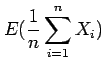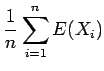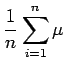Next: Example 2: The sample
Up: Accuracy and bias of
Previous: Accuracy and bias of
Contents
The expectation of the sample mean is calculated as follows:
Hence, the bias of the sample mean
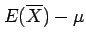 is zero
and the sample mean is an ``unbiased'' estimate of the population mean.
As discussed earlier, the variance of the sample mean is given by
is zero
and the sample mean is an ``unbiased'' estimate of the population mean.
As discussed earlier, the variance of the sample mean is given by
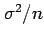 and, therefore, the MSE of the sample mean estimate is
simply given by
and, therefore, the MSE of the sample mean estimate is
simply given by
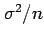 . As the sample size increases, the MSE
tends to zero and the sample mean estimate converges on the true population
value. This smooth unbiased convergence is what allows us to use
sample means to estimate population means.
. As the sample size increases, the MSE
tends to zero and the sample mean estimate converges on the true population
value. This smooth unbiased convergence is what allows us to use
sample means to estimate population means.




Next: Example 2: The sample
Up: Accuracy and bias of
Previous: Accuracy and bias of
Contents
David Stephenson
2005-09-30