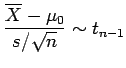Next: Z-test for non-zero correlation
Up: One sample tests in
Previous: Z-test on a mean
Contents
Does a sample come from a population with mean 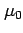 ?
?
Since the population variance is no longer known we must estimate it
using the sample variance 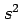 . This increases the uncertainty
and modifies the sampling distribution of the test statistic
slightly for small sample sizes
. This increases the uncertainty
and modifies the sampling distribution of the test statistic
slightly for small sample sizes 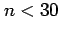 .
Instead of being distributed normally, the test
statistic is distributed as Student's t distribution
.
Instead of being distributed normally, the test
statistic is distributed as Student's t distribution
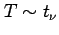 with
with 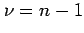 degrees of freedom.
Student's t distribution has a density
degrees of freedom.
Student's t distribution has a density
 ,
which resembles the normal density except that it has
slightly fatter tails (leptokurtic) and so provides more
chance of having values far from the mean.
This test is often referred to as
a one-sample t-test on the mean. Test using a T-score test statistic with the sampling distribution
,
which resembles the normal density except that it has
slightly fatter tails (leptokurtic) and so provides more
chance of having values far from the mean.
This test is often referred to as
a one-sample t-test on the mean. Test using a T-score test statistic with the sampling distribution




Next: Z-test for non-zero correlation
Up: One sample tests in
Previous: Z-test on a mean
Contents
David Stephenson
2005-09-30