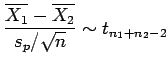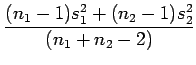Next: T-test on paired means
Up: Two sample tests
Previous: Two sample tests
Contents
Do two samples come from populations with the same mean ?
Two-sided test using a T test statistic
based on the difference in sample means that
has a Student's t distribution with 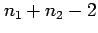 degrees of freedom
degrees of freedom
where
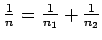 and
and 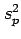 is
the pooled estimate of variance
is
the pooled estimate of variance
David Stephenson
2005-09-30