Do two paired samples come from populations with the same mean ![]() ?
?
Sometimes two samples are either generated or gathered as
pairs of values
![]() rather than as two separate
samples
rather than as two separate
samples ![]() and
and ![]() , e.g. heights of twins.
In this case, the two-sample
test on means described above is inappropriate and a paired
test has to be used. The paired test is based on testing the
mean difference of all pairs
, e.g. heights of twins.
In this case, the two-sample
test on means described above is inappropriate and a paired
test has to be used. The paired test is based on testing the
mean difference of all pairs ![]() for zero mean.
for zero mean.
| 0 | (6.7) | ||
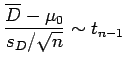 |