Linear regression

It is a reasonable hypothesis to expect that body height may be an important factor in determining the body weight of a Reading meteorologist. This dependence is apparent in the scatter plot below showing the paired weight versus height data

for the sample of meteorologists at Reading. Scatter plots are useful ways of seeing if there is any relationship between multiple variables and should always be performed before quoting summary measures of linear association such as correlation.

**Figure:** Scatter plot of body weight versus height for the sample of meteorologists at Reading. Best least squares fit regression line is superimposed.
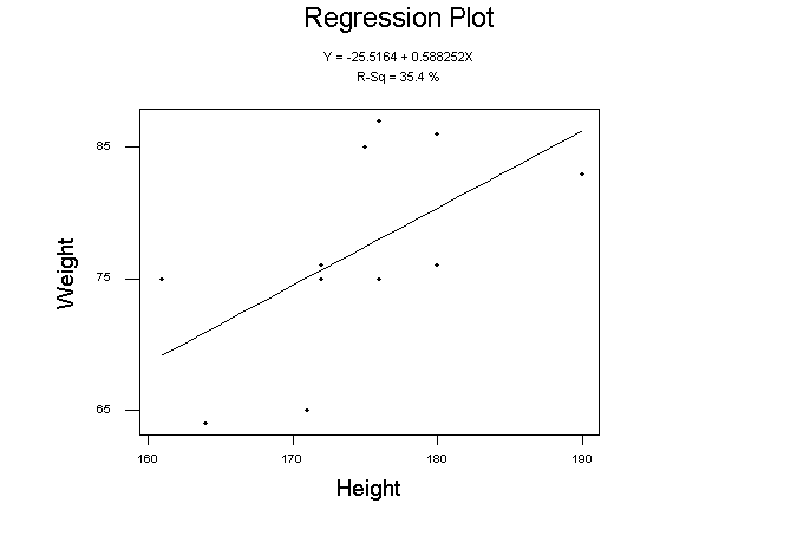$\begin{figure}\centerline{ \epsfysize=12cm \epsffile{dbsfigs/regression.eps} }\end{figure}$

The response variable (weight) is plotted along the y-axis while the explanatory variable (height) is plotted along the x-axis. Deciding which variables are responses and which variables are explanatory factors is not always easy in interacting systems such as the climate. However, it is an important first step in formulating the problem in a testable (model-based) manner. The explanatory variables are assumed to be error-free and so ideally should be control variables that are determined to high precision.

The cloud of points in a scatter plot can often (but not always!) be imagined to lie inside an ellipse oriented at a certain angle to the x-axis. Mathematically, the simplest description of the points is provided by the additive linear regression model

$\displaystyle y_i$

$\displaystyle =$

$\displaystyle \beta_0+\beta_1 x_i + \epsilon_i$

(7.1)

where $\{ y_i\}$ are the values of the response variable, $\{x_i\}$ are the values of the explanatory variable, and $\{\epsilon_i\}$ are the left-over noisy residuals caused by random effects not explainable by the explanatory variable. It is normally assumed that the residuals $\{\epsilon_i\}$ are uncorrelated Gaussian noise, or to be more precise, a sample of independent and identically distributed (i.i.d.) normal variates.

$\displaystyle Y\sim N(\beta_0+\beta_1X, \sigma^2_\epsilon)$

(7.2)

The model parameters $\beta_0$ and $\beta_1$ are the y-intercept and the slope of the linear fit, and $\sigma_\epsilon$ is the standard deviation of the noise. These three parameters can be estimated using least squares by minimising the sum of squared residuals

$\displaystyle SS$

$\displaystyle =$

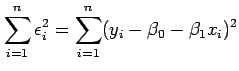$\displaystyle \sum_{i=1}^{n} \epsilon_i^2=\sum_{i=1}^{n} (y_i-\beta_0-\beta_1 x_i)^2$

(7.3)

$\displaystyle \frac{\partial SS}{\partial\beta_0}$	$\displaystyle =$	$\displaystyle -2\sum_{i=1}^{n}(y_i-\beta_0-\beta_1 x_i)=0$	(7.4)
$\displaystyle \frac{\partial SS}{\partial\beta_1}$	$\displaystyle =$	$\displaystyle -2\sum_{i=1}^{n}(y_i-\beta_0-\beta_1 x_i)x_i=0$	(7.5)

it is possible to obtain the following least squares estimates of the two model parameters:

$\displaystyle \hat{\beta_1}$	$\displaystyle =$	$\displaystyle \frac{s_{xy}}{s_x^2}$	(7.6)
$\displaystyle \hat{\beta_0}$	$\displaystyle =$	$\displaystyle \overline{y}-\hat{\beta_1}\overline{x}$	(7.7)

Since the simultaneous equations involve only first and second moments of the variables, least squares linear regression is based solely on knowledge of means and (co)variances. It gives no information about higher moments of the distribution such as skewness or the presence of extremes.