



Next: Weighted and robust regression
Up: Basic Linear Regression
Previous: ANalysis Of VAriance (ANOVA)
Contents
In addition to the basic summary statistics above, much can
be learned about the validity of the model fit by examining
the left-over residuals. The linear model is based on certain
assumptions about the noise term (i.e. independent and Gaussian)
that should always be tested by examining the standardized residuals.
Resisduals should be tested for:
- Structure The standardized residuals should be
identically distributed with no obvious outliers.
To check this, plot
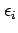 versus
versus 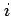 and
look for signs of structure. The residuals should appear to
be randomly scattered (normally distributed) about zero.
and
look for signs of structure. The residuals should appear to
be randomly scattered (normally distributed) about zero.
Figure:
Residuals versus order of points for the regression of weight on
height.
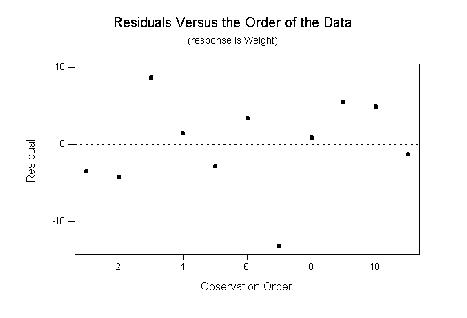 |
- Independence The residuals should be independent of
one another. For example, there should be no sign of runs of
similar residuals in the plot of
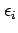 versus
versus 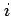 .
Autocorrelation functions should be calculated for regularly
spaced residuals to test that the residuals are not serially
correlated.
.
Autocorrelation functions should be calculated for regularly
spaced residuals to test that the residuals are not serially
correlated.
- Outliers There should not be many standardised
residuals with magnitudes greater than 3. Outlier points
having large residuals should be examined in more detail to
ascertain why the fit was so poor at such points.
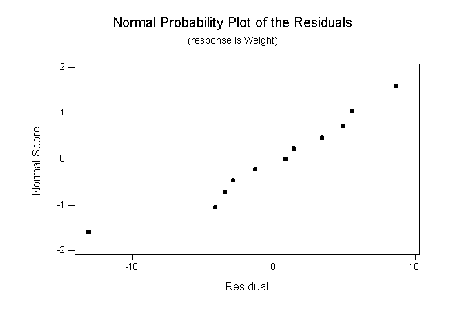
- Normality The residuals should be normally distributed.
This can be examined by plotting a histogram of the residuals.
It can be tested by making a normal probability plot in which the
normal scores of the residuals are plotted against the residual value.
Straight line indicates normal distribution.
Figure:
Normal probability plot of the residuals for the regression of weight
on height.
 |
- Linearity The residuals should be
independent of the fitted (predicted) values
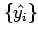 .
This can be examined by making a scatter plot of
.
This can be examined by making a scatter plot of
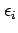 versus
versus
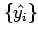 . Lack of uniform scatter suggests that
there may be a nonlinear dependence between
. Lack of uniform scatter suggests that
there may be a nonlinear dependence between 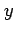 and
and 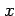 that
could be better modelled by transforming the variables.
For mutliple regression, with more than one explanatory variable,
the residuals should be independent of ALL the explanatory variables.
that
could be better modelled by transforming the variables.
For mutliple regression, with more than one explanatory variable,
the residuals should be independent of ALL the explanatory variables.
Figure:
Residuals versus the fitted values for the regression of
weight on height.
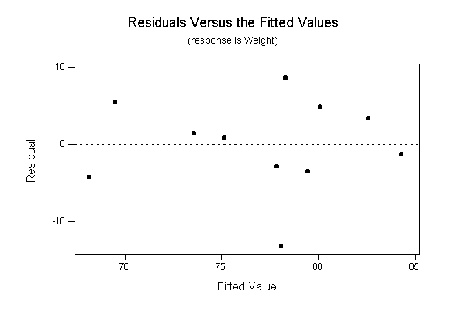 |
In addition to these checks on residuals, it is also
important to check whether the fit has been dominated
by only a few influential observations far
from the main crowd of points that can have high leverage.
The leverage of a particular point can be
assessed by testing the mean squared differences
of all the predicted values to leaving out this point
(known as Cook's distances).




Next: Weighted and robust regression
Up: Basic Linear Regression
Previous: ANalysis Of VAriance (ANOVA)
Contents
David Stephenson
2005-09-30