Non-smoothness in neural descriptions
What is non-smoothness?
Most mathematical descriptions of real world systems are smooth in nature, meaning that the things they describe vary continuously. One of the classic examples of such as system is a ball's flight through the air. Clearly, both the ball's trajectory and velocity are continuous. Now, imagine that the ball hits a wall and bounces back. Since the direction of motion has been reversed, so has the ball's velocity. If we look closely enough, we see that the ball deforms and the velocity changes smoothly. However, from further away, it appears that the change is instantaneous: this is the non-smoothness to which we refer.
Why do we use non-smooth descriptions?
Non-smooth descriptions often allow us to describe complex systems in a simpler fashion. For example, consider a plane coming in to land. When the plane's wheels are in contact with the ground, there is a frictional force acting upon them; when the wheels are off the ground, there is not. Similarly to the bouncing ball example, the plane's wheels will deform as they make contact with the ground, so in truth, the frictional forces do vary continuously. Whilst we can envisage mathematical descriptions that take this into account, it is easier to instead consider a system that switches from being frictionless to having friction instantly, in a non-smooth fashion.
Why don't we use non-smooth models all the time?
Whilst non-smooth descriptions can make the problem easier in some cases, in general, this is not true. For smooth systems, there are lots of nice mathematical results that we can use to study and make predictions about a given system. For example, these results allow us to predict the path of flight of a projectile, which is crucial if we want to launch rockets into space. The theory for non-smooth systems is vastly under-developed in comparison. The hope is that, in time, we will understand more about the non-smooth nature of systems so that we can develop simplifying approximations to them also. All of this typically means that we only use non-smooth approaches when they are very rapid changes in the model; so rapid that we can think of them of being instantaneous.
How is this relevant to neurons?
Much like the bouncing ball, nothing in a neuron is really non-smooth. The behaviour of any biological cell arises from biochemical reactions, from the level of genes, all the way up to complicated processes, such as cell division. For neurons, we are typically interested in how the voltage of a cell changes over time:
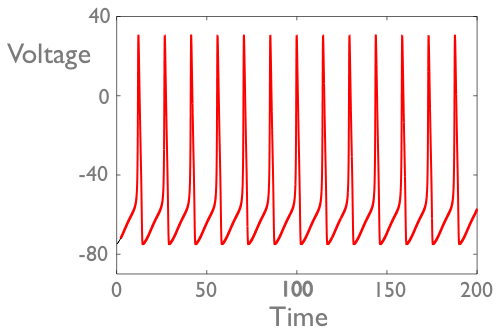 Neurons can be induced to fire action potentials as they receive current input from other cells. If the total input received is too small, the neuron will not fire. However, if the input exceeds a certain threshold, the neuron will. Since the time it takes to fire a single action potential is short compared with the rest of the neuron's behaviour, we can then use a non-smooth approach, just keeping track of whether the neuron is above threshold or not:
Neurons can be induced to fire action potentials as they receive current input from other cells. If the total input received is too small, the neuron will not fire. However, if the input exceeds a certain threshold, the neuron will. Since the time it takes to fire a single action potential is short compared with the rest of the neuron's behaviour, we can then use a non-smooth approach, just keeping track of whether the neuron is above threshold or not:
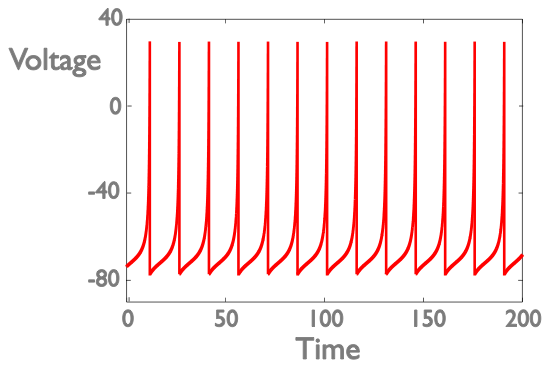
What are we doing in our research?
In our research, we are examining the consequences of using non-smooth approaches to study neural networks. As part of this, we need to look into when a non-smooth approach is appropriate, and when it might miss key aspects of the real neuron's behaviour. We do this both looking at individual neurons, but also when considering large networks of them. Studying large networks is particularly important since neurons only perform functional roles as part of a network. Moreover, because networks are harder to study than single cells, we can use the non-smooth approach to simplify our studies so that we can focus on specific aspects of the network, such as how the cells communicate with one another.