, we can work with the functions
and 
separately:
has only one singularity: a
simple pole at 0 with residue 1, so the product function there has a residue of
.
To determine the residues of , we
first consider the function
Here 
denotes Euler's
Gamma function.
Note: Riemann would have used different notation, and stated
. This is now more often denoted by
.
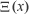We can also write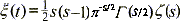 
where s = 1/2 +
it, which reduces the Riemann Hypothesis to
the assertion that all zeros of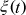 
are real.
Recall that this is the function with the simple functional equation
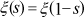
and whose only zeros are the
nontrivial zeros of 
. The trivial zeros are 'annihilated' by the
Gamma function
This is an integral function of order 1, meaning that its sequence of zeros {zn} is such that the sum of |zn| -a converges if and only if a > 1 (see Theorem 18, Ingham).
We further note that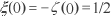 
(see Theorem
15, Ingham) and may now apply
Hadamard's Factorisation Theorem.
This gives us
Here bo and b1 are constants which
have yet to be determined, and the
are the zeros of 
, or equivalently, the nontrivial zeros of
.
Taking logarithms and then deriving gives
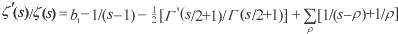
Letting s = 0, while observing that ,
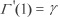(Euler's constant) and 
,
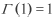we see that 
.
Note: The third term in this equation is expressible in terms of the digamma function (confusingly) notated
.
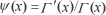Therefore we have
for a constant c. This is easily seen to have singularities at
s = 1 (residue = -1)
s = {-2,-4,-6,...} (trivial zeta zeros, residues = 1)
s = (nontrivial zeta zeros,
residues = 1)
Hence has the following
singularities and residues:
| singularities | residues |
| 0 (due to ) |
|
| 1 (due to pole of zeta function) | -x1/1 = -x |
| {-2,-4,-6,...} (due to trivial zeta zeros) | {x -2/2, x -4/4, x -6/6,...} which sum to [log(1-1/x2)]/2 |
| (due to nontrivial zeta zeros) |
 |
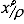This leads directly to the explicit formula. To summarise, the steps for
computing the residues are as follows:
1. Define in terms of
2. Apply Hadamard's factorisation theorem to get an expression
for in terms of an infinite product
over the nontrivial zeta zeros
3.Use this to produce an expression for in terms of the Gamma function and a sum over nontrivial
zeros.
4.Rewrite terms involving the Gamma function to give an expression
for in terms of sums over both
trivial and nontrivial zeros.
5.Calculate residues directly from definition.
back to proof outline
archive tutorial mystery new search home contact