the prime number theorem - a proof outline

This page is still in development, so it is debatable whether the current contents could be correctly described as a 'proof outline'. For now the idea is to provide a clear description of all of the key elements in the conventional proof. This is aimed at, for example, physicists who might have a recently developed interest in number theory, so that they can quickly get a basic understanding of why 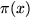~ x/log x and how/why the nontrivial zeros of the zeta function are involved.

The Prime Number Theorem (PNT) is an asymptotic law governing the prime counting function 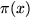. It simply states . This was initially an empirical observation, noticed by Gauss as a teenager after he had been studying a list of prime numbers.

[more]

It's not unreasonable to imagine that there might be some other way of counting primes, involving logarithmic weighting, so that the new counting function is asymptotic to the simpler function x.

This is indeed the case. If we define to be the function which counts each natural number n less than or equal to x with the von Mangoldt value

= log(p^k)/k = log(p) if n = p^k and zero otherwise,

then empirically we find . This is Chebyshev's psi function which, importantly, counts both primes and their powers.

[more]

It's not difficult to show the equivalence of the statements and . Hence to prove the PNT, we need only prove .

[more]

Taking the derivative of the logarithm of the Riemann zeta function (using its infinite product expansion), it follows easily that

where is the von Mangoldt function. The right-hand side is an example of a Dirichlet series.

Recall that .

[more]

Applying Perron's formula (a general result from the theory of Dirichlet series), we get the following formula involving a contour integral along the vertical line Re[s] = c in the complex plane:

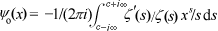
The function is a very slightly altered version of the function . At points of discontinuity, it has a value halfway between its limits on either side.

[more]

We can now evaluate the path integral in the above equation using a limit of expanding rectangular contours, the right-hand sides of which lie on the vertical line Re[s] = c. All singularities of the integrand function will eventually be enclosed in these contours, so the theory of residues can be applied. In this way we are able to obtain an expression for in terms of the (x-dependent) residues of the function .

This function clearly has singularities when s = 0 and when = 0. Recall that has both trivial and nontrivial zeros. Also, there is a singularity at s = 1, which is a simple pole of the zeta function itself.

[more]

This then produces the explicit formula

which is a sum of x-dependent residues, and is asymptotic to . Here the are the nontrivial zeros of the Riemann zeta function.

[more]

Now we need only make use of the properties and locations of the nontrivial zeros in order to deal with the term and show that it is well-enough behaved so that and hence as required.

In fact, it is sufficient to demonstrate that the nontrivial zeros all lie in the interior of the critical strip, that is, that has no zeros on the line Re[s] = 1.

[more]

important note: The PNT states that 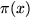~ Li(x), whereas the Riemann Hypothesis is equivalent to the statement 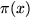= Li(x) + . This 'error term' in the PNT is intimately linked to the locations of the nontrivial zeros. The error term can be improved by restricting these locations - that is, by showing ever-larger regions of the critical strip to be zero-free. The Riemann Hypothesis proposes the ultimate restriction of the nontrivial zeros, or equivalently the maximal zero-free region of the critical strip.