Initially, by applying Cauchy's Residue Theorem we get the explicit formula in this form:

where the sum is over all zeros of the zeta function. Recall that

Note the factor of -1 in the relation

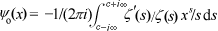
which results in the signs of the residues being reversed.

The above sum separates into two sums, over the trivial and nontrivial zeros respectively. The former sum becomes x ^-2/2 + x ^-4/4 + x ^-6/6 + ... This can be rewritten as

where the are now the nontrivial zeros of the zeta function.

"The 'explicit formula' suggests that there are connections between the numbers p^m (the discontinuities of ) and the [zeta zeros]. But no relationship essentially more explicit than this has ever been established between these two sets of numbers."

(A.E. Ingham, The Distribution of Prime Numbers)

There is another explicit formula worth noting, which relates to the "naive" prime counting function 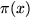more directly:

Just as - relates to , the function log() relates to the function which is given by the sum .

These variants - and log() on the zeta function are the generating functions of and l(n) respectively. As is the summatory function associated with , so is with l(n).

Recall that l(n) is defined to be 1/k in n = p^k, and to be zero otherwise.

The relevant explicit formula (also due to Riemann/von Mangoldt) is given by

Here relates to just as relates to .

It should also be noted that in both explicit formulas, the sum over nontrivial zeros of zeta is not absolutely convergent, so we must sum in order of ||. To be entirely rigorous, the sum should be expressed as a limit in this way.