Scroll Waves and Their  A Three-Dimensional Autowave Turbulence  A Three-Dimensional Autowave Turbulence

Introduction

The purpose of this paper is to describe basic features of the phenomenon of three-dimensional autowave (AW) turbulence. This interesting phenomenon provides an instructive example of spatio-temporal chaos, and may have useful applications. We believe that it deserves a peer study.

Turbulence is a term from hydrodynamics and so using it for autowave media is, of course, a metaphora. We use it to stress the essential properties of the phenomenon in question:

• It means complicated, apparently chaotic, spatio-temporal behaviour,
•  The complexity of behaviour grows with the size of the system, with other parameters unchanged,
•  It is related to vortex-like activity,
•  It is essentially a three-dimensional behaviour, qualitatively different from whatever may happen in the same system in two dimensions (hydrodynamists agree that `real' turbulence is essentially three-dimensional, unlike `weak' 2-D turbulence).

An AW medium is a 1 to 3-D continuum of points each exhibiting a special sort of nonlinear kinetics, and linked together via a diffusion-type process. These properties enable non-decaying propagation of nonlinear waves, called autowaves, which have their own inherent amplitude and form. At appropriate initial conditions, the autowaves may form `AW vortices' which have the form of spiral waves in two dimensions or scroll waves in three dimensions. These interesting classes of nonlinear waves were first observed in the Belousov-Zhabotinsky reaction [Zaikin & Zhabotinsky, 1970; Winfree, 1973], where the aforementioned nonlinear kinetics are autocatalytic oxidation of malonic acid. Since then, AW vortices were observed experimentally and predicted theoretically in a wide variety of systems of different physical nature [Swinney & Krinsky, 1991; Holden et al., 1991; Brindley & Gray, 1994]. A very important example is cardiac tissue [Gray & Jalife, 1996], where the nonlinear kinetics are the excitation (electric depolarisation) and recovery of cardiocytes' membranes, and the diffusion-like process is inter-cellular electric conductivity. AW media are most often described in terms of `reaction-diffusion' equations,

 

where 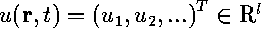 ,  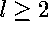, are concentrations of reagents,  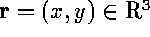, f(u) are reaction rates and  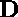is the matrix of diffusion coefficients. One of the `basic' AW models is the FitzHugh-Nagumo system of equations (FHN). In the form proposed by Winfree [1991] it reads

 

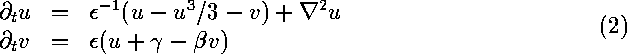
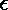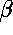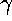where u(x,y,z,t) and v(x,y,z,t) are the dynamic variables and  ,  and  are constant parameters of the medium. Spiral wave solution for a biophysically detailed model of ventricular excitation is shown in Fig. 1.

  
Figure 1:  Snapshot of the spiral wave in a model of ventricular tissue of guinea pig (details described in Biktashev & Holden [1996]). Red component of colour coding shows the value of the transmembrane voltage, and green component that of one of the recovery variables. Two isolines of these two variables are shown in black. The blue ball at their intersection is the spiral tip. The blue line shows its trajectory over last few rotations. The spiral rotates counterclockwise, the rotation is not stationary but `meandering'.

The whole picture rotates counterclockwise around a region called core of the spiral. Far from the core, normal autowaves propagate formed approximately in the shape of an Archimedean spiral; within the core the behaviour is more complicated. The core may be defined as the region circumscribed by the tip of the spiral. The tip may be defined as the point where the propagation wavefront ends meeting the `waveback', or as an intersection point of two isolines, as in Fig. 1. As it is seen in the figure, the behaviour of the tip may be complicated, -- the so called meander. FHN model is a rough caricature of the ventricular model shown in this picture, which, in turn is a simplification of the reality, as it ignores completely the nontrivial spatial structure of the tissue. Nevertheless, during last 35 years, FHN model and its modifications were the most powerful heuristic tool for understanding the reentrant cardiac arrhythmias.

  
 Scroll Waves and Their  A Three-Dimensional Autowave Turbulence  A Three-Dimensional Autowave Turbulence
Fri Mar 20 12:57:08 GMT 1998