Mathematical models of excitable media take the form of reaction-diffusion systems of equations, and the generic reaction-diffusion system in a shear flow in the (x,y) plane can be written in the form
where u is the column vector of reacting species,
f represents the nonlinear reaction rates,
D is the diffusion matrix and 
is the gradient of the advection velocity, 
.
We assume that, for 
,
the (1+1)-dimensional version of this system has solutions
in the form of periodic waves (solitary waves, in the limit of infinite
period), with the speed and shape determined by the period
(or being unique for a solitary wave), which is
typical for excitation waves.
The analysis of the propagation of excitation in this system is readily performed for plane waves. It is easily seen that self-similar solutions are possible only for the trivial case of the wave propagating exactly across the flow. The generic substitution defining plane waves is
where the functions C(t), S(t) determine the
direction of propagation of
the waves, 
, and are defined up to a multiplicative
constant. We choose that constant so that at t=0, 
and
. To satisfy the system (1),
these functions must obey differential equations
and the wave profile must obey the (1+1)-dimensional PDE system
where the effective diffusion matrix K(t)D is determined by scaling factor K(t),
, and 
is the angle between the normal
to the wavefront and the x-axis (or between the wavefront and the
y-axis). In physical space, the dependence (5) corresponds
to a change of the distance between isophase lines according to the
equation (see Fig. 1):
The propagation angle at time t is
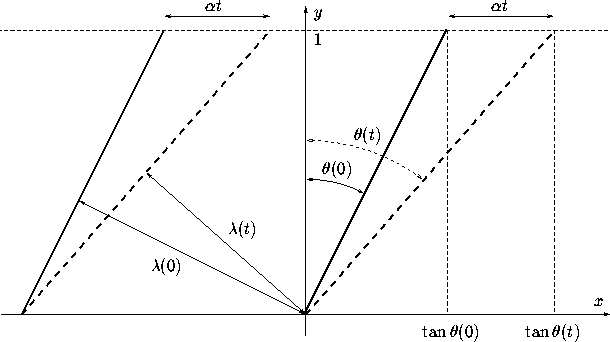
Figure 1:
Schematic diagram of the plane wave deformation by the shear flow.
Bold solid lines are equiphase lines at time moment 0, and bold dashed
lines are the same lines at time moment t.
Thus, for plane waves, the problem reduces to that for propagation of excitation waves in a 1-dimensional cable, with diffusion depending explicitly on time. Now we are going to study the conditions under which this dependence can cause a propagation block.
