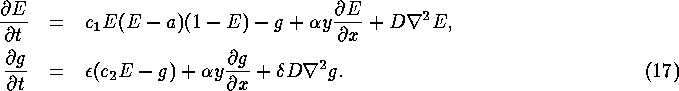
So far we have considered only plane waves. To verify the estimates and analyse the effect of the shear flow on more complicated autowave patterns, we have performed numerical simulations for the FitzHugh-Nagumo system with the flow incorporated, in the following form
We shall refer to the space and time units of this equation as s.u. and
t.u. respectively. The parameter values were chosen 
, a=0.02,
, 
, 
and D=1. We solved this system
with explicit Euler scheme (forward time, centered space), with space
step 
, in a rectangular medium
with periodic boundary conditions at
x=0,L and non-flux boundary conditions at 
. The sizes of
the medium, L and M, the velocity gradient, 
, and the time
step, 
, were varied in different experiments. The minimum
wavelength of a periodic train in quiescent ( 
) medium is
19.0, and the wavelength of the spiral wave is 41.0.
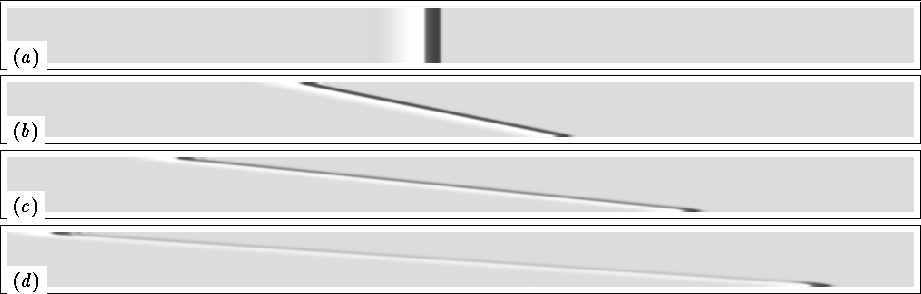
Figure 2:
Conduction block of a solitary plane wave in the linear shear flow.
Velocity gradient 
, medium size
,
time step 
Shown are snapshots of the E field (darker shade corresponds
to higher value) with interval 
.
Panel (d) corresponds to the moment just before the disappearance of
the wave: no excitation (black) and only the
recovery tail (lighter shade) left in the medium; some excitation
only survived near the boundaries.
The evolution of a solitary plane wave is shown in Fig. 2. The
horizontally propagating wave was initiated in the quiescent medium and
then the flow was switched on, which corresponds to the conditions of
the analytical estimation. The activator and inhibitor are E and g
and their characteristic times are, respectively, 
and 
According to (14),
this means that 
for our choice of
parameters. The threshold value of the velocity gradient necessary for
breaking a single plane wave was found numerically to be
,
the time 
and
the wave orientation at the moment of the break 
,
which, to this order of magnitude, is consistent
with the analytical estimates of
(14),
,
,
and
.
Figure 3:
Breakup of a spiral wave.
Velocity gradient 
, medium size
,
time step 
Shown are snapshots of the E field with interval 
We have studied what happens to autowave structures at velocity gradients
much less than this threshold. According to (15) and (16), we
have for this medium
,
and at
the wavebreak of the periodic train occurs at
at the angle of
.
These predictions, obtained for plane waves, agree, in order
of magnitude, with simulations of the evolution of more complicated
autowave patterns, the spiral wave and the target pattern.
In the first example, see Fig. 3, we initiated a spiral wave in a
quiescent medium ( ) and then switched on the shear flow. The
spiral wave breaks, and the time
( 
)
and orientation of the wave
( 
)
are in good correspondence with the theory. The correspondence in this
case would be better but for the phenomenon of ``plasticity'' of the
excitation wave: as the process is non-stationary, the visual break-up
happens later than the time at which conditions of stationary
propagation are violated. This explanation was confirmed by numerical
experiments when the flow was stopped before the wave broke, but after
it should have happened accordingly to the analytical estimate; the
wave subsequently broke, despite the absence of the flow.
Figure 4:
Breakup of a target pattern.
Velocity gradient , medium size
,
time step
Shown are snapshots of the E field with interval
In the other example (see Fig. 4), we initiated a series of
topologically circular waves by periodical stimulation of a point in
the medium, with the period equal to the period of the spiral wave. It
can be seen that while the first wave propagates without problems, the
propagation of the second is suppressed and the third wave is blocked.
This block occurs not for the whole wave but at some points only,
leading to wavebreaks which curl up into spirals. The first
breaks occur to the third wave, at time
, that is 
after its initiation,
and at a propagation angle of about
, i.e. the same as in the previous case.
These two examples show that, at least for the particular model chosen, the conditions of the wavebreak are almost the same whatever the origin and shape of the pattern is, and the order of magnitude of the velocity gradient necessary for the wavebreak agrees with the estimate (15) obtained for plane periodic waves based on the quasi-stationary arguments.
As we see in Fig. 3, a spiral wave, at time 
succumbs to
wavebreaks which then develop into new spiral waves. Thus, in a linear
shear flow a ``chain reaction'' of spiral wave births and deaths leads
to a ``frazzle gas'' of excitation wavelets. The mechanism for
generation of this ``frazzle gas'' is different from that described in
[9]. As this mechanism requires only a finite deformation of
the medium, we may expect that it can play its role not only in
constant flows, but in a more wide variety of situations. If oceanic
plankton dynamics are considered as an excitable medium [10] then currents can influence their spatial dynamics.
In a quite different physical context, cardiac muscle is excitable and is moving [11]. Condition (14) assumes the finite deformation of the medium to happen on the time scale of the fast excitation processes, about 1 ms in cardiac muscle, which does not seem realistic. Therefore, any normal motion of the heart is highly unlikely to break the excitation wave in it. On the other hand, the condition for breaking of repetitive waves (15,16) only requires finite deformation of the medium during any time period. The critical deformation is the ratio of the spiral wave period and the refractory period, which is known to be quite close to unity in cardiac tissue. Thus, while unlikely to cause the first breaking, the medium motion may play its role (along with other suggested mechanisms, such as heterogeneity and anisotropy of tissue properties, instabilities of plane wave propagation and scroll wave shape etc.) in the development of fibrillation once the reentrant activity has started and before the muscle has lost contractility. Naturally, the motion of the cardiac tissue is far from being constant linear shear flow, and therefore the results can only be considered as hints to what could be expected in more realistic models of reentrant activity in the heart involving mechano-electric feedback.
An ODE system of analogous form to the one considered in this letter, can also describe the action of an electric field on a chemical excitable medium, where the role of the advection velocity is played by the electric field multiplied by the mobility of the reagent. If all the reagents have the same mobility, the corresponding PDE system is formally equivalent to that for reaction-diffusion with convective flow. Examples of the nontrivial influence of the electric field on chemical excitable media are abundant and can be ``soft'', like modification of propagation velocity of waves and drift of patterns [12], or ``hard'', such as direction-dependent propagation block and splitting of excitation waves [13]. There is an interesting relationship between effects of curvature and electric current on excitation wavefront propagation [14]. Though the case of exactly equal mobilities is rather exotic (at minimum, it requires that all essential reagents have charge of the same sign), and the constant linear shear flow cannot correspond to a constant electric field (as the latter should be potential unless in presence of a nonstationary magnetic field), this analogy still might prove to be a powerful agent for mutual fertilisation of these two different problems. While the nontrivial effect of the electric field is due to the species-dependent variation of the advection velocity, the present study illustrates the effect of space-dependent advection velocity. In the context of this analogy, one hypothesis which can be put forward is that the quenching effect of electric field upon repetitive excitation waves might significantly depend upon the period of these waves -- a feature which, as far as we are aware, has not yet been appreciated.
