I. V. Biktasheva, Yu. E. Elkin & V. N. Biktashev
Institute for Mathematical Problems in Biology,
142292 Pushchino, Moscow region, Russia
Submitted to PRL 1997/08/04; Transferred to PRE 1997/11/21; Accepted 1997/12/01; Converted to HTML 1997/12/5
Dynamics of spiral waves in perturbed (e.g., slightly inhomogeneous) two-dimensional autowave media can be described asymptotically in terms of `Aristotelean' dynamics, so that the velocities of the spiral wave drift in space and time are proportional to the `forces' caused by the perturbation. These forces are defined as convolutions of the perturbation with the so called response functions. In this paper, we find the response functions numerically for the spiral waves in Complex Ginzburg-Landau Equation, and show that they exponentially decrease with distance.
PACS: 02.30.Jr, 02.30.Mv, 02.30.Sa, 02.60.Cb, 02.60.Lj, 64.60.Ht, 82.40.Bj, 87.10.+e
Spiral waves are observed in two-dimensional nonlinear active systems of various nature, e.g. Belousov-Zhabotinsky reaction [1] cardiac tissue [2], social microorganisms [3], neural tissue [4] and catalytic oxidation of CO [5]. They attract attention as model `self-organising' structures, and demonstrate remarkable stability. In this Letter, we show that spiral waves have a very selective sensitivity to perturbations.
Spiral waves are often studied in terms of `reaction-diffusion' PDE systems,
where 
,
is a
column-vector of reagent concentrations, 
are nonlinear reaction rates, 
is matrix of diffusion coefficients, 
and 
is a perturbation.
As shown in [6], if the last term in (1) is of a more
general form of parametric perturbation 
, this still reduces to (1) in the first order in
, so without loss of generality here we consider the
simpler form 
. Physical origin of the
perturbation may be various; the most frequent in applications is
inhomogeneity of medium parameters, but the analysis can be also
extended to external influence, anisotropy etc.
The simplest case of spiral wave is that of steadily rotating spiral,
where 
is its angular velocity and 
,
are polar coordinates. This may be
observed in perfectly homogeneous unbounded stationary media,
i.e. at 
. In presence of perturbations,
the spiral will drift in space
and accelerate or decelerate its rotation, i.e. `drift in
time'. This can be represented by
where 
is the vortex rotation centre and
is its initial rotation phase.
Asymptotic theory of such drifts has been developed in [6]. It
leads to `Aristotelian' motion equations, where the drift velocities are
proportional to the `forces', caused by perturbation 
,
In the first approximation, the forces are linear convolution-type functionals of the perturbation,
where 
is radius-vector in the frame of references attached to the spiral
wave, where polar coordinates are
We call kernels 
response functions (RFs). They determine the influence of particular
perturbations at a particular site and instant onto phase
(temporal RF, 
) and location (spatial RF,
) of the spiral wave. As seen in (5), graphs
of these functions rotate together with their spiral wave.
The RFs are interesting characteristics of the spiral wave. Known experiments and numerics may be interpreted so that these functions decrease with distance. This decrease may provide convergence of integrals (5) for non-localised perturbations, e.g. caused by variation of properties of the whole medium. The viewpoint of [7] was that these functions are asymptotically periodic, similarly to the spiral wave itself. Our viewpoint [8, 6] is that these functions should quickly decay. In other words, though spiral waves do not look like localised objects, they behave so in their dynamics. We are unaware of any attempts to prove or disprove this property directly.
In this letter, we study this question for the Complex Ginzburg-Landau Equation. This equation is one of the most `basic' equations of nonlinear science; another reason for this choice is its internal symmetry, which simplifies the analysis, reducing the two-dimensional eigenvalue problem to a one-dimensional one. For this model, we find the RFs numerically and show that they have the expected localised form.
Linearisation of reaction-diffusion system (1) on (3) in the frame of reference (6) leads to an equation with a time-independent linear operator
where
.
This operator has three neutral stability eigenvalues
corresponding to the translations in space and time, with the eigenfunctions, the `translation modes', being
The adjoint linear operator is
and its eigenfunctions
serve as projectors onto these modes, and are the RFs.
Requirement that 
in (3) is orthogonal to
leads to the motion equations (4) [6].
This equation can be written in the form
for 
with real parameters 
and 
. In
this letter, we restrict ourselves to the case of 
and
(and omit ). To apply the general theory of
[6] we first rewrite (12) in real vector
form[*]. Let us denote
Then equation (12), with added perturbation, takes the form
The unperturbed spiral wave solution (2) to (12) has the form
Here 
is a solution to the following boundary-value problem,
[**]
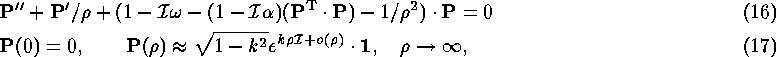where k is a nonlinear eigenvalue, and 
.
This problem was brought to a scalar form by substitution
with real
a and 
. Solutions to this problem were studied e.g. by
Hagan [9]; they are illustrated below by
figs. 2(a) (for 
and 
) and
3(a) (for 
).
It can be seen that due to the symmetry of (14) and (15),
the 
-valued RFs defined by (11)
have the form
This reduces the
two-dimensional problems for to one-dimensional
problems for functions 
:
It can be seen that if 
tend to zero as
, they do so exponentially, with decrement
being the smallest positive root
of the cubic equation
This requirement
makes problems (19,20) formally overdetermined, as
in fact they are EVPs, and that the eigenvalues are 
is only
our expectation. To make them numerically treatable, they
were re-formulated as EVPs with eigenvalues 
for n=0 (temporal mode) and
for n=1 (spatial
mode), and the smallness of 
,
and 
was considered
an estimation of the accuracy of the numerical procedure. The
problems were brought to real scalar form by substitutions
and
.
The half-infinite interval
was replaced by a finite interval
. Boundary conditions
A(0)=B(0)=C'(0)=D'(0)=0,
E(0)=D(0),
F(0)=-C(0),
and
were posed based on conditions (20)
via
asymptotics of acceptable solutions to the ODE system (19),
To select unique solutions of these homogeneous systems, we added
conditions B'(0)=C(0)=D(0)=1 , and normalised the solutions according to
(11) afterwards. Thus posed boundary-value - eigenvalue
problems have been studied in the double limit in the two numeric
parameters, the cut-off radius 
, and
the discretisation step 
. The discretisation was
second-order in h, and the solutions looked for should decrease
exponentially at large 
. Therefore, the expected behaviour of
the small eigenvalues is
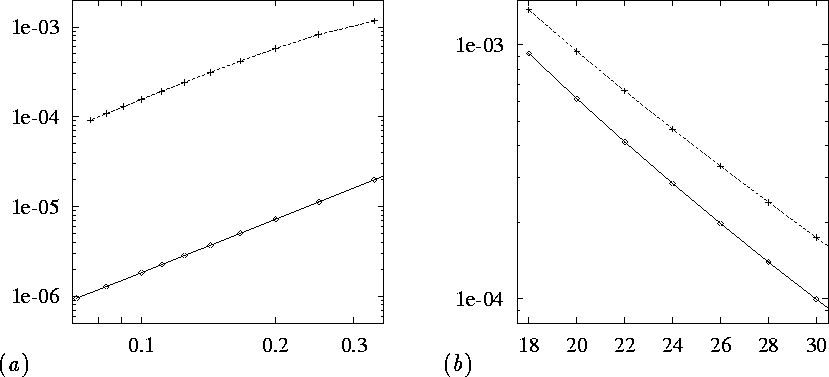
Figure 1:
The absolute values of the eigenvalues 
( 
) and
(+) as functions (a) of
discretisation step h, at 
, and (b) of
cut-off radius 
, at h=0.05.
This agrees well with the numerical results shown on
fig. 1, where the dependence on h is shown in
logarithmic, and on in semi-logarithmic coordinates, so
that the linear form of the graphs corresponds to the asymptotics
(22). We consider this as a numerical `proof' of existence of
solutions to the overdetermined problem (19,20). The solutions
are shown in fig. 2(b,c). Both temporal and spatial
RFs do decay quickly, being essentially non-zero only in the core.
The reconstructed shape of RF in the
(x,y)-plane is shown on fig. 3(b,c,d). Only
the first components are shown; the second components are the first
ones rotated in the (x,y)-plane by 
. The behaviour of the
RFs at other tested values of and was analogous; at
small 
, the spatial scale of all the functions grows
rapidly, which is consistent with Hagan's asymptotics [9].
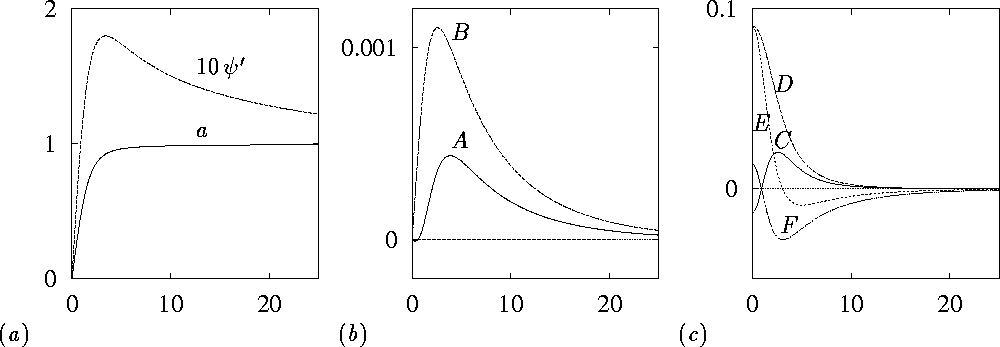
Figure 2:
(a) the nonlinear problem solution, (b) temporal mode
components, (c) spatial mode components, as functions of
.
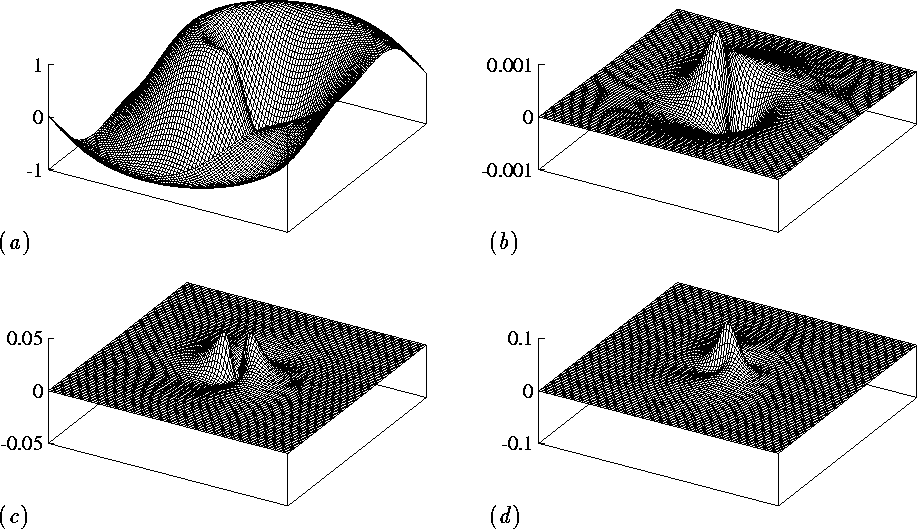
Figure 3:
(a) Spiral wave, 
, (b) temporal RF,
, (c) real-part of spatial RF,
, (d) imaginary-part of
spatial RF,
. Spiral wave length is about 67;
.
We have obtained numerically the response functions of spiral waves in
the Complex Ginzburg-Landau Equation. As expected, these functions are
localised around the core of the spiral, and decay exponentially
outside it. The spatial scale of localisation, 
, can be
found analytically from (21). Unlike solitons, spiral waves
look like essentially non-localised `objects'. On the other hand, their
dynamic properties, determined by the RFs, are those of localised
objects. This opposition between non-local appearance and infinity
region of influence, on one side, and local sensitivity and
independence on distant events, on the other side, makes spiral waves a
very interesting example of self-organisation pattern. We believe that
this physical property of localisation is mathematically expressed as
existence of eigenvalues 0 and 
of the adjoint
linearised operator in the space of functions integrable over the
plane, and is common for all `proper' spiral waves in generic
reaction-diffusion systems. The detailed conditions for this property
is a subject for further study, and here we have shown only the first
direct evidence to this viewpoint.
We are grateful to E.E. Shnol for encouraging discussions and valuable advice. This work was supported in part by grants from Russian Foundation for Basic Research (93-011-16080 and 96-01-00592) and Wellcome Trust (045192).
from (12), and i of the linearised theory,
with 
and 
. It has divisors
of zero, e.g., 
. We did not find in
literature if it has any special name.
