


Next: Feedback resonant drift monitored
Up: Results
Previous: Results
It has been long known that spatially uniform, periodic time forcing leads
to the motion of a rigidly rotating spiral wave. If the frequency of forcing
is close to the rotation frequency of the spiral wave, a circular, large
radius ``Larmor''-type drift results (motion equations of the rotation
center are similar to those of a charged particle in a magnetic field); if
the frequency is equal to the rotation frequency a linear, directed resonant
drift in a direction determined by the phase of the forcing results, Agladze
et al. [1]; Davydov et al. [13];
Biktashev and Holden [7]; Mantel and Barkley [18]. Figure
2
illustrates the boundary interactions of a resonantly drifting spiral. The
closer the resonantly drifting spiral wave approaches the boundary the
faster the core rotates (see 2(b) and (d)), hence the greater the changes
in the phase at which the constant frequency forcing is applied, and the
greater the changes in the direction of the drift. Fig. 2a shows that the
tip positions at which the forcing is applied move along a hypocycloid near
the boundary. In Fig. 2(a) the rotation of the core and the boundary induced
drift are opposite to each other while in (c) these coincide. Figures 2(e)
and (f) illustrate the effects of internal boundaries, or holes in the
medium. In (e) the resonantly drifting spiral is repelled by the hole of a
similar size to the core of the wave, and in 2(f) is captured by the
smaller hole.
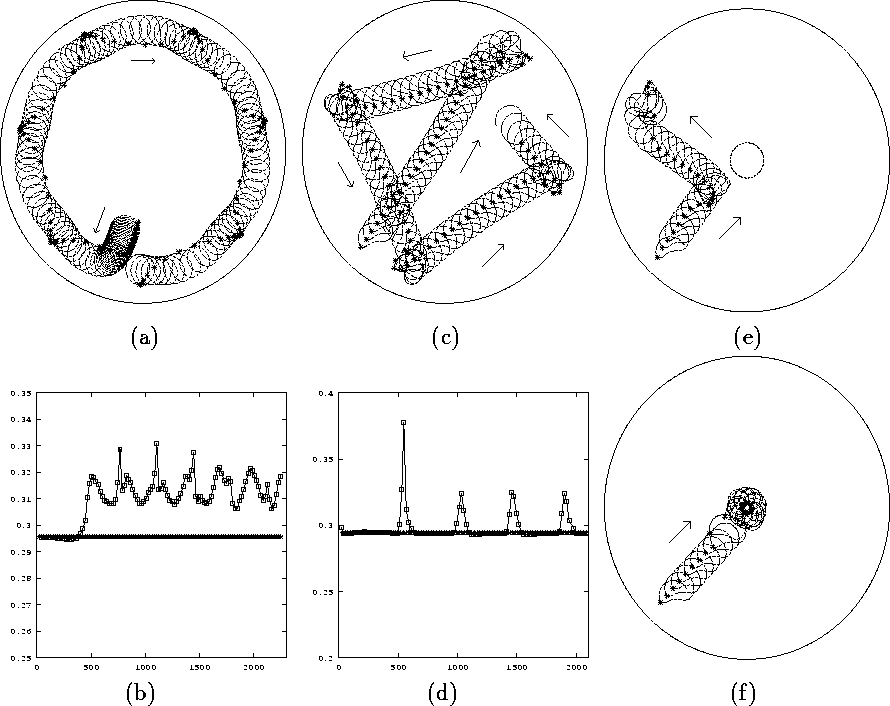
Figure 2: Tip trajectory of a spiral wave with drift induced by
spatially uniform periodic stimulation at a constant frequency.
In (a), (c), (e), and (f) the * marks the position of the wavetip at
the time when the perturbation is applied. (a) and (b) Stimulation with
amplitude A = 0.6. (c)-(f) A=2.5. (b) and (d) Dependencies of the
instantaneous frequency of the spiral's wavetip rotation on time.
"Squares" indicate the values of the instantaneous frequency of the
spiral, and the * indicate the stimulation frequency; (b) corresponds
to (a); (d) corresponds to (c). (e) Repulsion of the drifting spiral
wave by an obstacle in the medium, a hole with radius 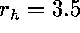 . (f)
Capture of the resonantly drifting spiral wave by a small hole of
radius
. (f)
Capture of the resonantly drifting spiral wave by a small hole of
radius 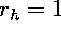 .
.



Next: Feedback resonant drift monitored
Up: Results
Previous: Results
Vadim Biktashev
Fri Apr 4 17:38:59 GMT 1997
