To initiate a spiral wave rotating near the centre of a circular medium, as
seen in Figure 1(a), an annulus with a small hole was used. Two
thin adjacent radial slices of a width about 
were set, one
corresponding to an excitation state with u=2.0 and v=-0.65; the other
corresponding to a recovering state with u=-2.0 and v=0.67; and the
remainder of the annulus was set to the quiescent state, u=-1.125 and
v=-0.65. These initial conditions gave rise to a rigidly rotating wave
attached to the hole, with the direction of rotation determined by the order
of the two slices. Setting the hole radius to 
resulted in a spiral
wave rigidly rotating around a point close to the centre of the medium. To
obtain a spiral wave with the wave tip close to the boundary, as shown in
Figure 1(b), external time forcing with a frequency equal to the
instantaneous rotation frequency of the wave was used, see (ii) in
Sect.2.6. The technique allowed us to place the core anywhere in the
medium by choosing different a number of stimuli, delay 
and forcing amplitude A.
An alternative way of spiral wave initiation can be found in, e.g. Zykov
and Müller [26]. In all the numerical experiments described below
spiral waves were rotating in the counter-clockwise direction.
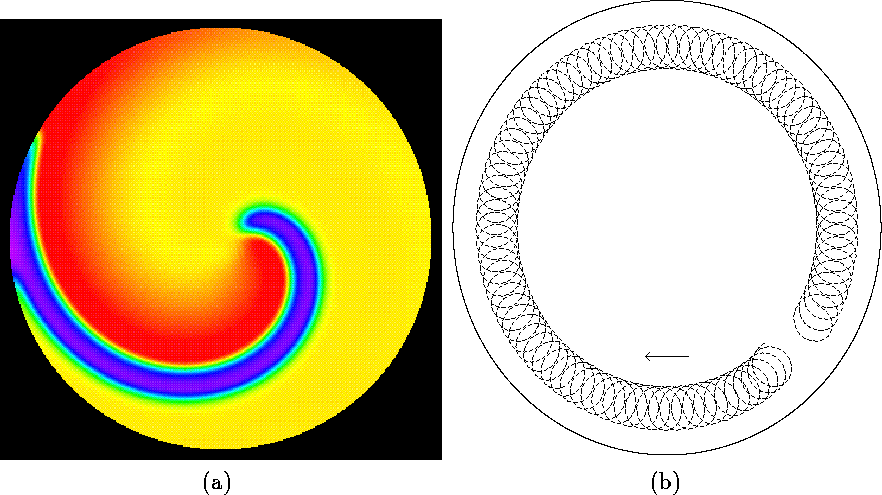
Figure 1: (a) Colour visualization
of the excitatory process u in a rigidly counter-clockwise
rotating spiral wave with the core of radius 
space units in
a circular domain of radius R=30 space units. (b) Biperiodic motion,
produced by boundary interactions. Shown is the tip trajectory of a
counter-clockwise rotating spiral wave which drifts along the boundary
in the clockwise direction.