The classical theory of Brownian motion considers it as a stochastic
process, i.e. as a motion driven by a random force that results from
the superposition of a large number of independent collisions.
Deterministic chaos has similar effects to a stochastic process, and
motion driven by a force depending on single low-dimensional chaotic
process can exhibit properties similar to those of stochastic Brownian
motion, e.g. mean walking distance 
, and is then called
deterministic Brownian motion or deterministic diffusion. A well
studied class of such processes, starting from the work [10],
are chaotic and periodic iterated maps; there the possibility of
macroscopic `diffusion' motion is provided by a noncompact discrete
group of translations. Here we deal with a continuous symmetry group
and continuous time, and will use a continuous version of corresponding
statements:
Theorem 1 Let a semi-flow 
in a Banach space 
be ergodic with an invariant measure 
, 
. Suppose a
function 
has a zero mean value in
,
and its autocorrelation function
quickly decays; more precisely,
Consider a point with coordinate 
moving with the velocity
V,
Then the mean squared displacement of the point in a given time interval t,
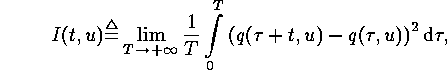
grows linearly at large t,
for almost all u with respect to .
If a stronger condition on the autocorrelation function is fulfilled,
then this estimation can be strengthened:
We did not find a proof of this statement in literature, and so we present it in the Appendix.
We assume that the invariant measure, ergodicity and quickly
decaying correlation function are consequences of a chaotic attractor
of the semiflow , though detailed specification of suitable
attractors would lead us away from the main subject.
Naturally, in case of nonzero 
, the mean square of the displacement
grows as 
, i.e. there is a directed drift with velocity
rather than Brownian walk. However, it is easy to see that if
other conditions of the Theorem are fulfilled, in the frame of
reference moving with velocity we shall observe Brownian walk
again. In other words, in general case there is a superposition of the
directed and Brownian motions.
